場の量子論の概略(2)
・ ゲージ理論とは?
ゲージ(物差し)原理とは、時空の座標の各点をごとに、回転や並進といった変換を施しても、その理論の式が変わらない(ゲージ不変)、という要求であり、それを満たす理論全体をゲージ理論という。通常は、単なる対称性を表わす”大局的”変換と区別して、”局所的”変換(変換のパラメーターが座標の関数である場合の変換)を、ゲージ変換という。
電子の場(電磁場)を考えると、実軸と虚軸を入れ替えてもその理論は変わらない。実軸と虚軸を入れ替える変換は、絶対値が 1 の複素数
クォークの場は、陽子(u、u、d)、中性子(u、d、d)のように、3つの成分を持つので、3×3行列を掛けることに対して大局的にゲージ不変であり、これは SU(3)変換と呼ばれる。これを、局所的にゲージ不変とすることに伴うゲージ場が グルオンであり、「強い力」を記述する。
陽子、中性子の崩壊などにかかわる「弱い力」は、2×2行列を掛ける SU(2)変換に伴うゲージ理論である。
特殊相対性原理では、たとえば スピンを測る x、 y、z 軸の向きをどちらにとっても良かったが、一般相対性原理を要求する、すなわち、各点で時空の軸の向きを取り替えても良いと要求するならば、その対称性に伴うゲージ場が必要となり、それが 「重力場」である。
したがって、自然界に存在する4つの基本的な力は、すべてゲージ場であることが知られている。
・ 力の統一理論とは?
力の統一理論では、ゲージ対称性を満たすことで力の統合が可能になる。
電磁力については、マクスウェルの方程式
次に、ゲージ対称性の要求から、① 電荷はどのような過程においても保存される、 ② 力を伝えるゲージ粒子(光子、ウィークボソン、グルオン)の質量は 0 、の条件が導かれる。しかし、弱い力を担うウィークボソンは大きな質量をもつので、条件②に反しゲージ対称性を破ってしまう。
そこで、”ゲージ対称性の自発的破れ”というメカニズムを使ってこの困難が解決された。(by. ワインバーグとサラム) 磁性体の自発磁化は、高温では無くなり対称性が高い空間になり、低温では小磁石が自発的に一定方向を向き 対称性が破れた空間になる。それと同じように、高エネルギー状態では弱い力のゲージ粒子は質量が 0 であり、通常の低エネルギー状態では、ヒッグズ機構(1964)により 質量を担うヒッグズ粒子をやり取りして、ウィークボソンは質量を持つようになる。(ただし、ヒッグズ粒子は様々な素粒子に質量をもたらすと言われているが、未だ観測されていない。) エネルギーが100GeV以上の領域では、電磁力は”原始の電磁力”、弱い力は”原始の弱い力”としてほぼ同じ大きさとなり同一レベルで扱われ、このようにして、電弱力として統合される。(100GeV以下では、ヒッグズ粒子の影響を受け質量を得る。)
この統一理論で統一された力の対称性は、 SU(2)×SU(1) となる。
さらに、大統一理論では、SU(3) の強い力が統一され、エネルギーが 1016GeV 以上で真空の相転移が起こり、光子(γ)や 3種のウィークボソン(w+、w-、Z0)はもとより、強い力を担う 8種のグルオンと 12種の x 粒子(クォークとレプトンの交換に関わる)の質量がすべて 0 になり、対称性 SU(5) という、より高い対称性が成立すると予想されている。
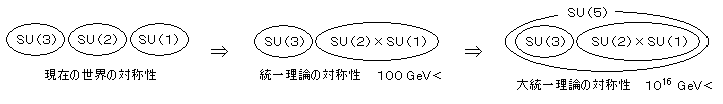
しかし、大統一理論によると、陽子の平均寿命は 1032年であり、スーパーカミオカンデ(東大・宇宙線研、神岡、地下1100m・5万トンの水・1万本の光電子倍増管)中の水10000トン(約1034個の陽子・中性子)は、100個/年の陽子崩壊が起こることになるが、1996年4月からの実験では未だ観測されていない。これは、大統一理論に修正を迫るものであり、陽子の寿命を延ばすために ”超対称性”という概念が検討されている。
まず、荷電対称性は、通常のスピン量子数と区別して、仮想的な荷電空間での回転を”荷電スピン量子数”(=アイソスピン)として導入し、核子の量子状態の新しい解釈とする。(中性子が -1/2、 陽子が +1/2、 π-、π0、π+ がそれぞれ -1、0、+1) これは、電磁力はエネルギー、エネルギーは質量だから、陽子、中性子、3つの π 中間子の質量は異り(陽子-中性子:0.1%、π 中間子:3%の差)、荷電対称性は破れ 異なった粒子として存在するが、元々は同じ粒子であるとするものである。このように、フェルミ粒子(スピン半整数)とボーズ粒子(スピン整数)が”超粒子”という基本粒子の異なる状態であると考え、フェルミ粒子の半整数スピンを上向き、ボーズ粒子の整数スピンを下向きとする”超対称性スピン”を導入する。
ただし、大統一理論がどのようなゲージ対称性を持つべきかという問題には、未だ答えが出ていない。
これに、さらに、重力の統一を加えた統一理論が検討されているが、未だ完成度はきわめて低い。この統一理論は、宇宙のインフレーション時の4つの力の分化の仮説と相まって研究されている。
4. 電磁相互作用とゲージ不変性:
アハラノフ-ボーム効果(AB効果)の発見により、電磁場には より根源的な場であるベクトルポテンシャル A が存在することが明らかになった。電子の磁気的な相互作用を記述するのに、相対論的な量子力学では、旧来のマクスウェル方程式を修正する必要がある。
上記の、自由ディラック方程式で、
(A→ : ベクトル・ポテンシャル、Φ : スカラー・ポテンシャル 、 D→ 、Dt : 共変微分)
が得られる。
すると、磁気モーメントとの相互作用
クライン・ゴルドン方程式についても、同様の置き換えを行なうと、
この置き換え
電磁相互作用、強い相互作用、弱い相互作用、重力は、すべてゲージ理論として統一的に理解できる。
5. U(1)ゲージ理論: (以下、自然単位系で表示)
U(1)変換(ユニタリー(1)対称=複素数
すると、ゲージ場 Aμ は、共変微分がこの変換則を満たすようにゲージ変換のもとで変化する。
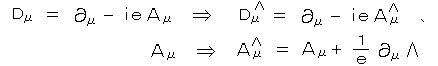
この局所対称性をゲージ対称性、Λが座標による場合の φ、Aμ の変換をゲージ変換という。
たとえば、クライン・ゴルドン方程式
ゲージ場の強さを、
このゲージ場の強さ Fμν を用いて、古典的 U(1)ゲージ理論のゲージ場を満たす運動方程式は、
Fμν が ゲージ場 Aμ で
この運動方程式が、電磁気学の運動方程式に対応することを示す。
電磁気学の場合、 Fμν は 電場 E と 磁場 B 、-e jν は 電荷密度 ρem と 電流密度 j em に、
ゲージ場 Aμ は スカラーポテンシャル Φ と ベクトルポテンシャル A→ に、
ポテンシャルと電磁場との関係は、
マクスウェル方程式も、上記の運動方程式は電磁気学との対応によって書き換えられ、
また、
ゲージ電荷が Q のとき、共変微分は
ゲージ変換による物質場は、
のように変換される。このとき 電荷のみが変化し、ゲージ場は変わっていない。 今までの議論の電子は Q = -1 の場合であり、 u クォークは Q = +2/3、 d クォークは Q = -1/3、 原子核は Q = N(原子番号)、などとなる。
6. 量子電磁力学:
電荷をもつ粒子(フェルミオン; 電子、陽電子、μ粒子、・・)の場と ゲージ場の量子である光子との相互作用を扱う。
相互作用の強さは、
1) 電子-光子散乱; 散乱過程で相互作用を2回するので、散乱振幅 α とすると、散乱断面積は
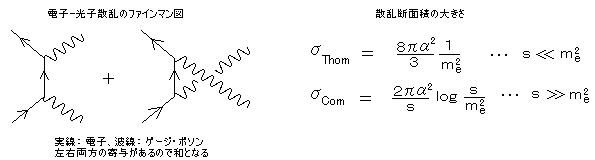
* 注) ファインマン図は、縦軸が時間、横軸が空間、反粒子は時間を逆行する粒子として表わされているが、素粒子の反応と行列要素の関係を表現するためのものであり、粒子が時間を逆行することを表わしているのではない。
2) μ 粒子(e+ + e- → μ+ + μ-): 電子と陽電子が反応して、μ 粒子と反μ 粒子(μ粒子は電子の質量の200倍)を対生成する、高エネルギー過程を考える。
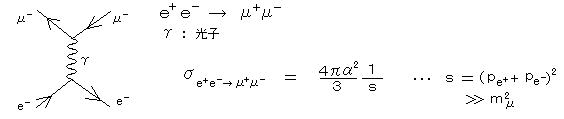
電子と陽電子から、電荷 ±Q e をもつ粒子 X とその反粒子 X- が生成する場合は、
3) ポジトロニウムの崩壊: 電子と陽電子の束縛状態であるポジトロニウムは、対消滅して n 個の光子となる。ポジトロニウムは水素原子と同様に、全角運動量 j、軌道角運動量 l、スピン s という離散的なエネルギー準位をもつ。崩壊の平均寿命は、
基底状態: 1S0 (j = 0、l = 0、s = 0) → 2γ、 τ(2γ) = 1.25×10-10(s)
第1励起状態: 3S1 (j = 1、l = 0、s = 1) → 3γ、 τ(3γ) = 1.41×10-7(s)
電磁相互作用により光子 n 個 に崩壊する分岐幅
崩壊幅(=単位時間に反応が起こる率=平均寿命の逆数)は、
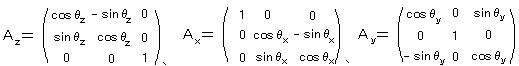 であるが、積についての交換は、
であるが、積についての交換は、 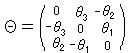 であり、
であり、