零点振動　　　・・・　調和振動子モデルによる



　　１．　１次元調和振動子の量子化：


　　調和振動子モデルは、バネの先に重りがついている振動を扱い、質点の変位 ｘ にその力が比例する（ｆ ＝ − ｋ ｘ、 ｋ： バネ定数）ので、水素原子のように中心からの距離に反比例するポテンシャルが存在する場合と異なっている。しかし、調和振動子は厳密に解け、ある状態からのわずかなずれを調べたり、場の量子論の自由場が調和振動子の無限個の集まりと考えることができるなど、量子力学の一つの基本モデルとして非常に便利である。この自由場は、互いに結合していない調和振動子がいくつあっても、何次元の空間であっても、１次元の１個の調和振動子の単なる和として扱うことができる。

　　古典論の運動方程式とその解は、力の定数を　ｍω2 として、　
　　　　　　　　　　　　となる。

　　　　　　　　　　　　　　　　　　　　　　　　　　ただし、　Ｔ： 周期、ν： 振動数、 ω ＝ ２π/Ｔ ＝ ２πν ： 角周波数（ｏｒ 円振動数）


　　ここで、運動の対称性、系の取りうる状態、物理量の取りうる値などを調べることができるように、ラグランジアン Ｌ と ハミルトニアン Ｈ を求める。
　　この運動方程式を、オイラー-ラグランジュ方程式　　として与えるようなラグランジアンは、

　　　　　　　　　　　ととることができる。 Ｌ は明らかに、 ｑ　→　−ｑ　（空間の反転）に対して 不変である。

　　次に、ｑ に対して正準共役な運動量を求めると、　　　　であり、量子化してハミルトニアンを求めると、
　　　　　　　、　　　　　となる。




　　２．　シュレディンガー表示による解法：


　　このハミルトニアン　　に対して、固有値 Ｅ の定常状態を　｜ 〉　とすると、
　　　となる。これと、座標 　の固有値 ｑ をもつ固有状態　〈ｑ｜ との内積をつくり、波動関数を　ψ（ｑ） ＝ 〈ｑ｜ 〉 とすると、シュレディンガー方程式（１次元）

　　　　　　　　　　　　　　となり、　物理的な解の境界条件は、　ψ（±∞） ＝ 0　である。


　　ここで、シュレディンガー方程式を次のように書き直す。
　　　　　　　　　　　　　　　・・・・・　（１）

　　この第２項の係数が　ｑ　→　±∞　で発散するから　ｑ ＝ ±∞ がこの微分方程式の特異点である。｜ｑ｜が大きいとき ε は充分小さいので、
　　　　　　　　　　　　　　　　　　を考えればよい。

　　　　　　とおくと、　　となり、｜ｑ｜ が大きい領域では　　は近似解であり、境界条件を満たすのは、複合で負にとった方である。
　　そこで、解を、ｆ（ｑ） を ｜ｑ｜ が大きいとき ψ（ｑ） の ｑ 依存性をガウス型からあまり変えない関数として、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・・・　（２）　　　　

　　とおく。　これを（１）に代入すると、　ｆ’’ − ２αｑｆ’ ＋ （ε − α）ｆ ＝ 0　　となって 係数の中の最も大きな特異項 （−α2ｑ2） が消えている。

　　ここで、さらに、変数と関数を　　のように変換すると、

　　　　　　　　　エルミートの微分方程式　　　　

　　として知られる微分方程式になり、その解は、　　ε/α − １ ＝ ２ ｎ　　（ｎ ＝ 0、1、2、・・・）　　のときだけ エルミートの多項式 とよばれる ｎ 次式 で与えられ、それ以外のときは無限級数になる。
　　これは ｄＨ/ｄξ、Ｈ の係数が整関数の２階微分方程式だから、べき級数を用いて解を求めることができる。

　　　とおいて代入すると、　漸化式　　　　　　　　　　　・・・・　（３）

　　が得られるから、 ａ0、 ａ1 が決まればすべての ａｎ が決まる。

　　もし、この級数が無限級数であれば、これは ｎ の大きな値によって決まるから、　ａｎ＋２ ≒ （２/ｎ）ａｎ　を級数
　　　と比べると、
　　　　より、Ｈ（ξ） は ξ が大きいとき　　で表わされる。
　　　しかし、（２）より、　　となって、境界条件　ψ（±∞） ＝ 0　を満たさない。
　　ゆえに、物理的解は、Ｈ（ξ）のべき級数が有限次で切れるようなものである。

　　これは、漸化式（３）より、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ε/α ＝　２ ｎ ＋ １ 　　　　　　　　　　　　　　　　　　　　　・・・・　（４）

　　を満たし、　ｎ が偶数ならば ａ1 ＝ 0 、 ｎ が奇数ならば ａ0 ＝ 0　であるようなものである。この条件を満たす式を、
　　　　　　　　　　　エルミートの多項式　　　　という。

　　（４）より、ｎ 番目の状態に対するエネルギーの固有値は、
　　　　　　　　　　　　　　（ｎ ＝ 0、1、2、・・・）　　・・・・　（５）


　　その固有値に対する 固有波動関数は、（２）から、
　　　　　　　　　　　　　　　　　　（Ｎｎ： 規格化定数）　　の形をとる。

　　この規格化定数を求めるために、　Ｈｎ（ξ）の生成関数　　　を用い、
　　もう一つ　　　をつくって、次の積分を計算する。

　
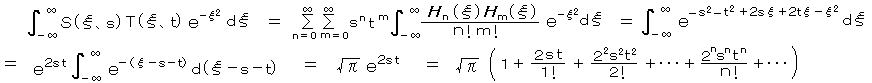
　　この第２辺と第６辺を比べると、
　　　　　　　　　　となるから、
　　したがって、固有波動関数の直交性　　　　　が示され、
　　　　　　　　　　　　　　規格化定数は、　　　　　　　となる。




　　３．　零点振動とその検証：


　　量子化した調和振動子のエネルギーの固有値（＝期待値）は、２．の（５）より、
　　　　　　　　　　　　　
　　ここで、ｎ ＝ 0 、すなわち、エネルギー最低の状態　Ｅ0 でも、調和振動子は静止ではなく一定の振動をしている。
　　これを、零点振動（れいてんしんどう、Zero-point motion）といい、そのエネルギー　　を零点エネルギーという。

　　調和振動子の ｎ 番目の状態での 運動量と位置の ０ からのずれの平均は、（＊ハイゼンベルク表示で計算され、）それぞれ、
　　　　　　　であり、 ｎ ＝ 0 になっても、
　　　　　　が残っている。これは、古典論（の極限）では存在しなかった振動である。


　　　（　注）　このエネルギー最低の状態を便宜的に”真空”と呼ぶ慣習があるが、場の量子論の”ディラックの海”や”負エネルギー解”についても同様に数学上の便宜的なものであり、その実態についてはこの議論のみでは分からない。　→　近年、カシミール効果の実証（３．（３））によって、真空（電磁場の真空）は、２枚の金属板間と周りの真空との零点振動エネルギー密度の差が有限の値となり、真空は 常に仮想光子が生成・消滅している場であることが証明された。）


　　 ＊　零点エネルギーの期待値： 〈Ｅ〉0 ＝ ω/２）”が、量子化された磁束の振動（振動数 ＝ （ ｌ ａ 〉、ｌ ｂ 〉 状態のエネルギー差）/）を測定することによって、磁束に関するマクロの不定状態として観測されるはずである。これは、”シュレディンガーの猫”である マクロのコヒーレンス状態（ＭＱＣ）である。ただし、零点振動はあまりにも微弱であり、散逸過程での損失が大きく現在のところ測定は成功していない。

　　＊　また、不確定性原理によって零点振動は絶対零度においても存在するので、液体ヘリウムが常圧で固化しない原因になっている。（液体ヘリウムを３５気圧以上にすると、固化してｂｃｃ構造の ３Ｈｅ になるが、零点振動による格子振動の振幅は格子間隔の４０％にもなる。そのため、格子点にある波動関数の重なり合いが無視できなくなって、数万回に１回の割合で純粋に量子論的なトンネル効果により原子どおしが入れ替わる。）

　　

　　　　　　　　　　　　　　　　　１．へ戻る　　　　　　　　　　　　　　　　　　トップへ戻る