重力場の方程式 と その解
1. アインシュタインの重力場方程式:
重力場は、計量テンソル gμν で表わされる。与えられた重力場 gμν のもとでの質点の運動方程式を調べ、 gμν を決定するための方程式(重力場の方程式、あるいは、アインシュタイン方程式)を求める。
質点の軌道 xμ(τ) を 固有時 τ の関数として決定するために、 ① 運動方程式が一般座標変換のもとで形を変えないこと、 ② 等価原理を満たしていること、 の2つの条件を満たす必要がある。また、③ 重力場が弱い場合は、質点の運動が非相対論的であり、近似的にニュートンの運動方程式になるはずである。
③の条件より、まずニュートン・ポテンシャルを満足する方程式を調べる。ニュートンポテンシャルは、質量 mi (i = 1、・・・、N) の質点が ri の位置にある場合、 単位体積あたり ρ(r) の質量が連続的に分布している場合、 それぞれ、
後者の場合、ポアソン方程式は、
となり、質量密度がポテンシャル φ を決定する。(∇2 は、平坦な空間におけるラプラス演算子) 一般相対論において、このポアソン方程式に相当する式を求める。
特殊相対論で導かれた 電磁場中のエネルギー運動量テンソルを、一般相対論の場合に拡張するために、次のように定義する。
ただし、
一般相対論においては、特殊相対論におけるエネルギー運動量保存則
となる。
上記ポアソン式(1)に対応する式は、計量 gμν についてせいぜい2階微分までを含むとする。gμν の1階、2階微分に関して線形であるのは、リッチのテンソル R、スカラー曲率 R を含む gμνR 、および gμν しかないので、
保存則(2)は、計量テンソルの共変微分=0 であることを用いて、
したがって、重力場の方程式は、
ただし Λ = -c3/c1 、 k = k’/c1
とおける。(Λ は宇宙定数)
k の決定は、弱い重力場の場合に(3)がポアソン方程式(1)と一致することによって行なう。
(3)の左辺を整理し、R を消去して R のみとし、gμν を掛けて μ、ν についての和をとると、 -R - 4Λ = -kgμνTμν となる。これを R について解き、(3)に代入すると、
ここで、弱い重力場とは、gμν がミンコフスキー空間からあまりずれていないという意味なので、 gμν = ημν + hμν とおいて、1次の項のみを残す近似とする。接続係数
リーマンの曲率テンソル
となる。
さらにここで、μ = ν = 0 、かつ、時間変化の無い”静的”な場合( hμν の時間変化 = 0 )に限定すると、(4)は、
質点系がほとんど静止している場合は、エネルギーテンソルは質量のみにより、T00 ≒ ρc2 、 Tij = T0i ≒ 0 (ρ:質量密度)だから、
重力場が弱く、運動が非相対論的な場合の
したがって、(3)の重力方程式は、
あるいは、宇宙定数 Λ を取り入れた場合、
となる。(6)、(7)とも アインシュタイン方程式と呼ぶ。
アインシュタイン方程式は、(光も含めた)物質のエネルギーと運動量が存在する点で、それが原因となって時空が曲がる(リッチ曲率をもつ)ことをあらわし、時空の幾何学的性質はその中にある物質によって規定されることを意味している。 また、宇宙定数は、宇宙論を扱う際に必要で、観測宇宙論によって決めるしかない。
2. シュバルツシルドの解 と ブラックホール:
静的中心対称な重力場の解を、シュバルツシルドの解(厳密解)という。原点にのみ質量 M があるとして、そのまわりの計量を正確に求めることができる。原点以外ではエネルギーテンソルは 0 だから、解くべき方程式は原点以外で、
すなわち、リッチテンソル = 0 (リッチ平坦)の条件となる。
極座標を用い、時間によらない(静的な)、球対称な解(計量 gμν は動径 r のみの関数)を求める。未知関数を ν(r)、λ(r) として、
とおく。
この計量の接続係数
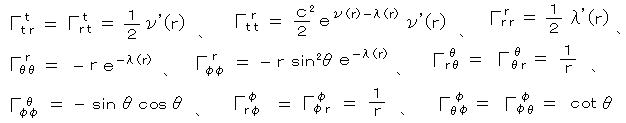 ・・・ (9) であり、
・・・ (9) であり、その他の成分は 0 となる。
リッチのテンソルは、
(10)① と (10)② より、 λ’ + ν’ = 0 、 これを (10)③ に代入すると、
e λ = 1 - 1/2 rλ’ + 1/2 rν’ = 1 - rλ’ = e λ・d/dr(re- λ) となり、
を得る。 a、b は任意の定数であるが、b = 0 としても一般性を失わない。
したがって、計量は、
r が充分大きく、非相対論的な
これが質量 M がつくるポテンシャル φ = -GM/r であるから、
となる。
(* シュバルツシルド半径は、太陽質量(1.99×1030kg)で2.94×103m、地球質量(5.98×1024kg)で8.86×10-3m程度になる。)
ニュートン力学では、星からロケットが脱出できる条件は、 1/2mv2 > GMm/R より、c2 > v2 > 2GM/R 、すなわち、 R > 2GM/c2 となる。
(9)に
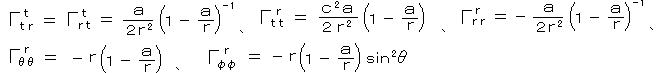 となって、
となって、測地線の方程式の t 方向の成分は、
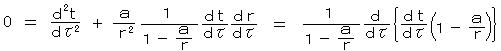 となる。
となる。したがって、
t と τ との関係
が得られる。 k は、無限遠 r = ∞ での 座標時 t と 固有時 τ の差を与える時間の遅れ因子であり、さらに、無限遠で質点が速度をもてば、
k = 1/√(1 - v∞2/c2) になる。
測地線の方程式の θ 方向の成分は、
ここで、初期条件 θ = π/2 、dθ/dτ = 0 とすると、常に θ = π/2 となるから、
この場合の φ 方向の測地線の方程式は、
が得られる。これは、ニュートン力学で中心力場での角運動量保存則が r2dφ/dt = h となることに対応している。
さて、r 方向の測地線の方程式を解くために、τ が固有時であり、 ds2 = -c2dt2 から、 θ = π/2 を線素の式に代入すると、
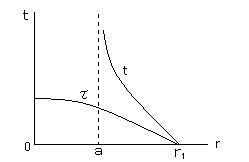
静止している質点が r > a の領域から出発して、原点 r = 0 へ動径沿いにまっすぐ落ちていく場合(h = 0)を考える。(k = 1、v∞ = 0)
τ で測定した場合: r1 から r まで運動するのに要する時間 τ は、
であり、 r < a でも成り立ち、有限の時間内に r = a を通過する。しかし、
t で測定した場合: 所要時間 t は、
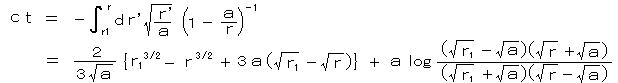
であるが、 r → a の極限では t → ∞ となるので、 無限遠にいる観測者がこの質点を見るとき、r = a に接近するのに無限に長い時間がかかっているように見える。
また、光の進路は、 ds2 = 0 によって決まるので、動径方向の線(θ、φ = 一定)に沿っての進路は、
となって、 t で時間を測定すると、 r = a に到達するとき、質点の場合と同様に無限の時間がかかる。
そして、r < a の領域からの光は届かないことになり、この領域を ブラックホール、 r = a という面を 事象地平面という。
* 回転を含む解:
回転を伴う場合、カー解(厳密解)として知られている解は、
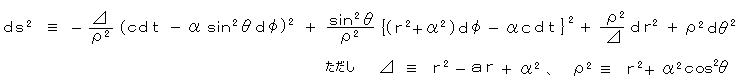
ここで、a = 2GM/c2 、および、 α がこの解を特徴付ける解である。 α = 0 ならば、シュバルツシルドの解に一致する。
この解の物理的洞察を得るため、近似して見やすくする。 α2 << r2 、 α2 << ar として、α について1次の量のみを残せば、
となる。
((注) 遠心力は2次なのでこの議論はできない)
この線素の近似式より、計量テンソルが φ に依存していないので、この空間は φ → φ + 定数 という変換に対して不変、すなわち、中心に位置する質点が θ = 0 の軸(z 軸)の周りに自転するような角運動量を持つ。この近似式は、シュバルツシルドの解(11)において、
(この一般相対論の効果は、与えられた物体の慣性力は、宇宙全体の質量(正確には、エネルギー運動量テンソル)によって決定されるとした、いわゆる”マッハの原理”の考え方を、正確な方法で言い表わしているともいえる。)
3. 星の重力平衡と重力崩壊:
中性子星は、電子と陽子が逆ベータ崩壊( e- + p → n + νe )を起こして中性子になった星で、白色矮星よりも高密度で 太陽と同程度の質量が半径10km程度の大きさに収まっている。中性子同士は、強大な重力による圧力にもかかわらず、フェルミ統計に従う粒子(フェルミ粒子)がもつ縮退圧によって支えられている。
白色矮星までの密度の星については、ニュートン力学による 球対称の星の重力平衡の式、
星の状態方程式 P = K ρ1+1/n (K、n は r によらない定数) では、星の中の電子のフェルミ運動量を pF として、
|pF| << mec (me :電子の質量)、すなわち、星の密度がある程度低い場合、
|pF| >> mec 、すなわち、星の密度が高い場合、
ここで、後者の場合について、 r → ξ 、 ρ(r) → θ(ξ) と変数変換した、
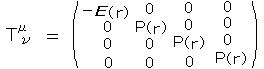 とおく。また、エネルギー運動量の保存則に対応する条件は (2)の、 ∇μTμν = 0 である。
とおく。また、エネルギー運動量の保存則に対応する条件は (2)の、 ∇μTμν = 0 である。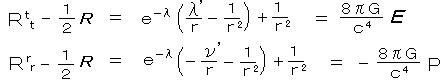 ・・・ (14)
・・・ (14)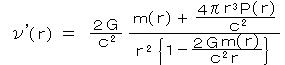 となるから、これを(16)に代入すると、
となるから、これを(16)に代入すると、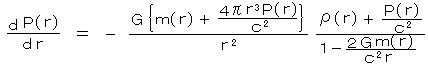 ・・・・ (17)
・・・・ (17)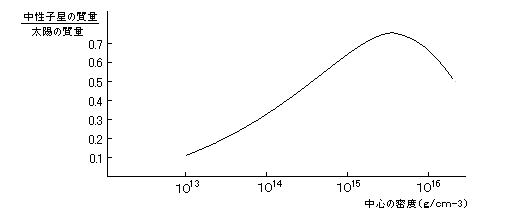
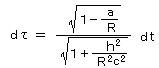 となる。
となる。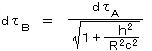 、 GM/Rc2 = 6.95×10-10 、
、 GM/Rc2 = 6.95×10-10 、