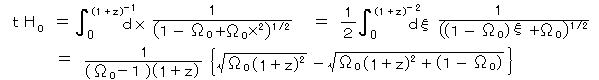膨張宇宙の理論?
ハッブルの法則?の発見(1929)、宇宙背景輻射の発見(1965・ペンジャンスとウィルソン)等の基礎の上に、現在の”ビッグバン宇宙論”と呼ばれるものが形成されていった経緯がある。 このうち、一般相対性理論と関連の深い部分のみを列挙し、膨張宇宙論の物理的な特性を調べ、この理論の結果が観測結果と矛盾していることを見る。
1. 4次元空間中の3次元曲面(リーマン幾何学より):((注)これは純粋な数学)
3次元の線素の一つとして、
とおく。 f(r) = 1 ならば通常のユークリッド空間になる。
接続係数のうち 0 でないものは、
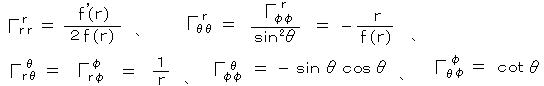 、
、リーマンの曲率テンソルは、
リッチのテンソルは、
(0 でないもの) である。
したがって、空間の曲がりを表わす スカラー曲率は、
特別な場合として、この曲率がすべての空間部分で定数(定曲率空間)の場合、 f(r) と R が決まり、
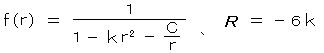 となる。 C は任意定数で、 C が 0 でないと f(r) は r = 0 で 0 となり、線素 ds2 が縮退するので、 C = 0 とおく。
となる。 C は任意定数で、 C が 0 でないと f(r) は r = 0 で 0 となり、線素 ds2 が縮退するので、 C = 0 とおく。k = 0 の場合、 f(r) = 1 より、通常の3次元ユークリッド空間になる。
1) k > 0 の場合;
4次元ユークリッド空間 (x、y、z、w) の中の3次元球面を、次のように書く。
これは、3次元極座標(r、θ、φ)で記述すると x = r sinθ cosφ、 y = r sinθ sin φ、 z = r cosθ、 w = √((1/k) - r2) であるから、
線素
で表わされる3次元空間全体の体積は、
計量テンソルの行列式が
となって有限である。
体積が有限であるとは、これが閉じた空間になっていることを表わし、測地線も無限に伸びることは無い。( 0 < r < 1/√k)
ここで、θ、 φ が定数で、r の方向に伸びる測地線を考えると、(τ を測地線のパラメーターとして、)
となる。これは、パラメーター τ が増大する方向に測地線をたどっていっても、sin カーブに従ってある地点で r が減少する方向に反転する。それは、τ = τ0 での初期速度 C’ の大きさによらない。
2) k < 0 の場合;
r の領域は制限無しで、3次元曲面の体積は無限大になる。 測地線の方程式の解は、
となって、r は τ の増大と共に指数関数的に無限遠まで伸びている、開いた空間になっている。(2次元曲面の”鞍形”に相当する)
2. 宇宙の観測結果による仮説:(これ以降は、仮説に無理があるので要注意!)
(1) 多くの銀河からの光のスペクトルが、赤方に偏移している事実があり、 1+ z ≡ λ0/λ で定義される量 z を レッドシフト という。
この解釈として、ドップラー効果によって”遠くにある銀河ほど速い速度でわれわれから遠ざかっている”、という宇宙モデルが考え出され、銀河までの距離 dL と その後退速度 v との間には、 v = H0dL という単純な比例関係が成り立つという、ハッブルの法則(1929)と呼ばれるものが提唱された。ただし、ごく近い星雲中のセファイド(ケフェイド)型変光星の変光周期という”経験則”によって距離が割り出されるのみであり、遠い星雲までの距離の測定は不可能なので、この結果から外挿して他の大部分の星雲までの距離を予想しているに過ぎない。 このハッブル定数 H0 (しばしば h = H0/100で表わす)は、長い間 観測グループ間の食い違いがあったが、なぜか 最近は収束して、
H0 = 71±7(km・s-1・Mpc-1) 、(h = 0.71±0.07)、 1Mpc = 3.2615×106光年 = 3.0856×1022m
という(もっともらしい)値になっている。この逆数 H0-1 ≒ 138億年 が、宇宙の年齢の目安とされ、この爆発的大膨張による宇宙の創成の仮説は ”ビッグバン” と呼ばれている。
(2) また、宇宙のどの方向からも等方的な強さの電磁波がやってくる 宇宙背景輻射が発見(1965)され、黒体輻射の温度として T = 2.7277±0.002 K (約3K)である。その輻射の等方性はきわめて精度がよく、方向による温度のゆらぎは、 ⊿T/T ≒ 10-5 程度しかない。
これは、創成当時の宇宙に熱平衡状態にあった光が、ビッグバンによって広がった現在の宇宙に 均一かつ等方的に満ちていると解釈されている。
((注) ビッグバンと言っても、3次元宇宙のどこかに爆発の中心があるのではなく、その中にある均一性・等方性を保ちながら、4次元空間の中の3次元の事象の地平線が一様に広がったことを主張している。)
一様・等方性とスケール因子の導入: まず、3次元空間の一様性と等方性を仮定して宇宙の構造を調べる方法を”宇宙原理”と呼ぶ。この宇宙原理を満たす時空の計量は、FRW計量(フリードマン-ロバートソン-ウォーカー計量)と呼ばれているものがあり、次のものである。
ただし、 a(t): 膨張宇宙の時刻 t によるスケール因子、 k : 空間の開閉を決める定数 ・・・・ (6)
この計量の3次元空間部分の性質は、1.の(2)を調べたとおりである。実は、一様・等方性を満たす計量はこの(6)以外には無い。等方性についての自由度を調べると、
r = (x1、x2、x3) = (r sinθcosφ、r sinθsinφ、r cosθ) という座標に対し、3次元回転の直交行列 Rij を用いて、
また、
このように、回転の自由度3個と 並進の自由度3個の、合わせて6個の自由度の数だけ計量の形を変えない変換が存在し、3次元空間の場合、これが最大限 対称な空間であることが知られている。(N次元空間の場合、 N(N + 1)/2 個の計量の形を変えない キリング・ベクトル が存在する。)
スケール因子と レッドシフト、ハッブル定数との関係: 光の経路は、 ds2 = 0 だから、光が r 方向へ進むとして、(6)で dθ = dφ = 0 とした式を積分して、
すると、 δt /a(t) = δt0 /a(t0) となり、光の波長の比は周期 δt0 、δt に等しいから、レッドシフトを z として、
1 + z = λ0/λ = a(t0)/a(t)
を得る。
a(t) を現在の時刻 t0 付近でテイラー展開すると、 1/(1+ z) = a(t)/a(t0) = 1 + H0 (t - t0) - 1/2 q0 H02 (t - t0)2 + ・・・
となるが、ここで、
を定義している。この H0 が ハッブル定数、 q0 が 減速パラメーター を表わし、膨張宇宙のスケール因子 a(t) との関係となっている。
3. フリードマン方程式と宇宙論モデル:
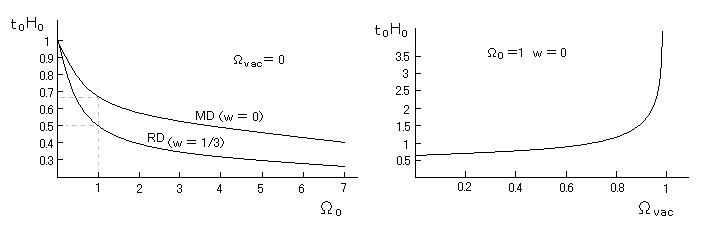
比較的少数のパラメーター(ハッブル定数 H0 、減速パラメーター q0 、エネルギー密度 Ω0 、宇宙定数 Ωvac 、(バリオン数と光子の数の比 η )など)によって、初期宇宙を記述することができる。
まず、FRW計量(6)を、アインシュタイン方程式
に代入して、膨張宇宙のスケール因子 a(t) を具体的な関数形として求める。エネルギーテンソル Tμν は、等方性より、
 を用いる。 (E は物質のエネルギー密度、 P は圧力)
を用いる。 (E は物質のエネルギー密度、 P は圧力) また、これらの量は、一様性より、座標によらず、時間のみによるとする。(cf. 中性子星内部のエネルギーテンソル)
FRW計量(6)から、 接続係数(0 除く):
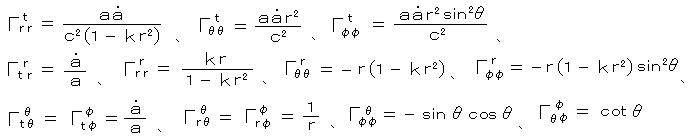
リッチのテンソル:
スカラー曲率:
(μ、ν) = (t、t) の成分は、
(μ、ν) = (r、r)、(θ、θ)、(φ、φ)の成分は、
次に、 ∇μTμt = 0 という条件を与えると、これは a(t)3 に比例する微小体積中において、エネルギー変化と圧力 P が釣り合っている条件を表わしている。
・・・・・・ (8)
初期宇宙論では、物質のエネルギー密度 E と圧力 P との間には、 P(t) = wE(t) という形の状態方程式を考える。
釣り合い式 (8)にこれを代入すると、 E(t) ∝ a(t)-3-3w という比例関係となるが、w の値によって次のように呼ばれる。たとえば、w = 1/3 の輻射優勢の場合は、P = 1/3E となって 質量の無い光子の集団の状態方程式と同じで、質量に比べ充分大きなエネルギーをもった状態である。これはエネルギー運動量テンソルのトレース Tμμ = 0 となる条件である。
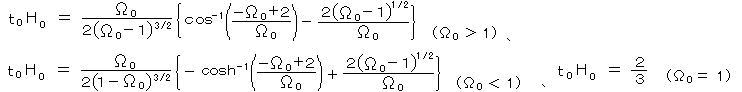 ・・・ (11)
・・・ (11)