自然数論における不完全性定理の証明（抜粋）：



　　Ｓ を 数記号をもつ理論とする。
　　　かつ　　であるような式 Ａ が存在するとき、 Ｓ は ω‐矛盾 を含むという。 このような Ａ が存在しないとき ω‐無矛盾 という。

　　数論的述語　Ｗ 、Ｗ* を次のように定義する。
　　　　　　、
　　　　　　
　　Ｗ、Ｗ* は再帰的述語であるから、Ｎ の中でそれらを表現する式が存在する。それらを Ｗ、Ｗ* （自由変項 ｘ、ｙ）とすると、
　　
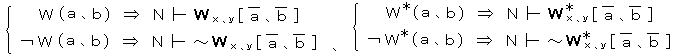
　　が成り立つ。

　　式 　の ゲーデル数を ｎ とする。その式の自由変項 ｘ に 数記号 ｎ−を代入して、閉式 Ｇ をつくると、　　
　　述語 Ｗ と 自然数 ｎ の定義より、Ｗ（ｎ 、ｂ） が成り立つのは、ｂ が Ｇ （＝ ゲーデル数 ｎ の式に含まれるゲーデル数２３の自由変項に数記号 ｎ−を代入して得られる式） の証明のゲーデル数であるときである。
　　ゆえに、　Ｗ（ｎ 、ｂ） ⇔ ｂ　は Ｇ の証明のゲーデル数である。


　　ゲーデルの第１不完全性定理：

　　　　　　　　　�@　　Ｎ が無矛盾であるならば、Ｇ は Ｎ で証明可能ではない。
　　　　　　　　　�A　　Ｎ が ω‐無矛盾であるならば、〜Ｇ は Ｎ で証明可能ではない。

（証明）
　　�@　　Ｇ が Ｎ で証明可能であると仮定して、Ｎ が矛盾を含むことを示す。
　　　であるならば、Ｎ における Ｇ の証明が存在する。 Ｇ の証明のゲーデル数を ｐ とすると、Ｗ（ｎ、ｐ） である。 ゆえに　である。
　　ところが、論理的公理により、　　より、　　となって、Ｎ が矛盾を含むことになる。

　　�A　　Ｎ が ω‐無矛盾であると仮定する。このとき Ｎ は無矛盾でもあるから、�@によって、Ｎ における Ｇ の証明は存在しない。 ゆえに、　である。ゆえに、
　　である。
　　Ｎ は ω‐無矛盾であるから、　ではない。　ゆえに、〜Ｇ は Ｎ で証明可能ではない。


　　理論 Ｓ のすべての閉式 Ａ について、　または　　であるとき　Ｓ は完全であるという。
　　　でも　　でもないような閉式 Ａ が存在するとき　Ｓ は不完全であるという。


　　数論的述語 Ｆｍｌ（ａ）、Ｐｆ（ｂ、ａ） は再帰的述語であるから、Ｎ の中にそれらを表現する式が存在する。それぞれを表現する式　Ｆｍｌ（自由変項 ｘ）、Ｐｆ（自由変項 ｙ、ｘ）とすると、
　　
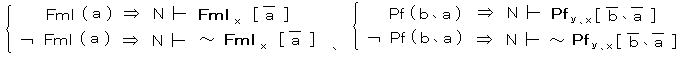
　　が成り立つ。この Ｆｍｌ、Ｐｆ を用いて Ｃｏｎｓｉｓ なる閉式を作ると、
　　　　　　　　


　　ゲーデルの第２不完全性定理：

　　　　　　　　　　　Ｎ が無矛盾であるならば、Ｃｏｎｓｉｓ は Ｎ で証明可能でない。

（証明）
　　第１不完全性定理の�@より、Ｎ が無矛盾であるならば Ｇ は Ｎ で証明可能でない、が言える。この証明の全過程を理論 Ｎ の中で形式化することにより、
　　　　　　　　　　　　が得られる。（証明略）
　　（Ｇ は Ｎ で証明可能でない、を表す式は Ｇ 自身である。）
　　ゆえに、　　ならば　　である。ところが、Ｎ が無矛盾であるとき、　でないから　　でない。

　　　　　　　　　　　　　　　　　　戻る