丂丂丂丂丂丂丂丂丂俀丏丂僎乕僨儖偺晄姰慡惈掕棟
丂丂恖娫偼丄偳偙傑偱乭抦傞乭偙偲偑偱偒傞偺偩傠偆偐丠
丂丂俛丒儔僢僙儖偵傛傞偲丄楌巎忋偺揘妛幰偨偪偺庡挘偡傞丄偙偺乭擣幆榑乭偺栤戣偼丄亀棟惈庡媊亁 偲 亀恄旈庡媊亁偺俀偮偵戝暿偝傟傞丅 僇乕僩丒僎乕僨儖偼丄慜幰偺棟惈庡媊偺棫応偐傜 悢棟榑棟妛偲偄偆 巚嶕偺嵟傕怺偄偲偙傠傪尩枾偵捛媦偟丄偦偺偙偲偵傛偭偰 偐偊偭偰 晄姰慡惈掕棟偵傛傞恖娫棟惈偺尷奅偑柧傜偐偵偝傟偨丅偟偐偟斵帺恎偼丄乮幚嵼榑幰傾僀儞僔儏僞僀儞偺塭嬁傕偁偭偰乮仏乯乯 惗奤丄乭崌棟庡媊揑乭側乮亖 晄姰慡惈掕棟偲柕弬偟偨乯悽奅娤傪帩偭偰偄偨丅乮偙偺娫堘偭偨怣擮偵屌幏偡傞偙偲偼丄寢嬊丄僎乕僨儖帺恎傪惛恄揑攋柵傊捛偄傗偭偨丅乯
丂丂乮侾乯丂僎乕僨儖偺晄姰慡惈掕棟丗
丂丂乭尵梩乭傗乭悢妛乭偺榑棟揑崪巕偼婰崋壔偟偰偡傋偰尩枾偵埖偆偙偲偑偱偒傞丅
丂丂弎岅榑棟偲偼丄屆揟揑側乭柦戣榑棟乭傪奼挘偟偰丄庡岅丒弎岅偵偁傞検壔偝傟偨柦戣偵偮偄偰傕婰崋壔偟偰尩枾偵埖偆傕偺偱丄擔忢尵岅偵偍偗傞 偁偄傑偄偝傗懡媊惈傪旔偗丄堦掕偺岞棟偲悇榑婯懃傪恖岺尵岅偵傛偭偰尩枾偵峔惉偡傞傕偺偱偁傞丅乮婰崋楍傪堄枴榑忋偺晛捠偺暥偵栠偡偙偲傪乭夝庍乭偲尵偆乯
丂丂僎乕僨儖偼丄乭弎岅榑棟偺僔僗僥儉 俽 偵偍偄偰丄偡傋偰偺柦戣偑寛掕壜擻乮徹柧壜擻乯偱偁傞偙偲乭丒丒丒乭姰慡惈乭傪徹柧偟偨丅乮弎岅榑棟偺姰慡惈掕棟乮1929乯乯 偙傟偵傛偭偰丄弎岅榑棟偺偡傋偰偺懨摉側悇榑婯懃偑岞棟壔偝傟摼傞偙偲偑柧傜偐偵側偭偨丅斵偼丄傾儕僗僩僥儗僗埲棃偺榑棟妛傪姰惉偝偣偨偺偱偁傞丅
丂丂堦曽丄悢妛偵偮偄偰偼丄僸儖儀儖僩乚傾僢僇乕儅儞偺岞棟宯偑採埬偝傟偨丅偡傋偰偺悢妛偼丄岞棟揑廤崌榑 偲偄偆 偦傟埲忋扨弮壔偱偒側偄宍幃偵娨尦偝傟傞丅偙偺岞棟宯偺宍幃揑側婰崋楍傕堄枴榑忋偺夝庍偵傛偭偰悢妛偵帩偭偰偄偔偙偲偑偱偒傞丅乮1928乯
丂丂偲偙傠偑丄悢妛偵偮偄偰偼丄偦偺傛偆側姰慡惈偑惉棫偟側偄偙偲偑丄晄姰慡惈掕棟乮1931乯偵傛偭偰柧傜偐偵偝傟偨丅 乮悢妛偺晄姰慡惈丄偁傞偄偼丄柍恠憼惈乯丂堦斒偵丄僔僗僥儉 俽 偑惓忢偱偁傞偲偒丄恀偱偁傞偵傕偐偐傢傜偢 俽 撪晹偱偼徹柧偱偒側偄傛偆側柦戣乮僎乕僨儖柦戣 俧乯偑懚嵼偡傞丅丂偡側傢偪丄
丂丂戞堦晄姰慡惈掕棟丗丂僔僗僥儉 俽 偑惓忢偱偁傞偲偒丄俽 偼晄姰慡偱偁傞丅
丂丂戞擇晄姰慡惈掕棟丗丂僔僗僥儉 俽 偑惓忢偱偁傞偲偒丄俽 偼 俽 帺恎偺柍柕弬惈傪徹柧偱偒側偄丅
丂丂晄姰慡惈掕棟偼暋悢偺掕棟偺廤崌偱偁偭偰丄僆儕僕僫儖偺 帺慠悢榑偺亀冎柍柕弬惈亁乮僎乕僨儖丄1931乯偵偮偄偰偺晄姰慡惈偑丄亀扨弮柍柕弬惈亁乮儘僢僒乕丄1936乯偺晄姰慡惈偵奼挘偝傟丄偝傜偵丄亀恀棟惈亁乮僞儖僗僉乕丄1936乯丄亀寁嶼壜擻惈亁乮僥儏乕儕儞僌丄1936乯丄嵟嬤偱偼 亀儔儞僟儉惈亁乮僠儍僀僥傿儞丄1989乯側偳偺傛偆偵晄姰慡惈偺斖埻偑奼挘偝傟偰偄偭偨丅
丂丂晄姰慡惈掕棟偑摫偄偨偺偼丄偨偲偊偽丄帺慠悢榑偺柍柕弬惈傪徹柧偱偒側偄偙偲偱偼側偔丄帺慠悢榑偺柍柕弬惈傪乭帺慠悢榑撪晹偱乭徹柧偱偒側偄偙偲偱偁傞丅偙傟偼 俽 亄 俧 偵僔僗僥儉偺斖埻傪峀偘偰傕怴偨側僎乕僨儖柦戣 俧乫 偑弌尰偟丄偳偙傑偱傕摨偠帠偺孞傝曉偟偱偁傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮丂仺丂丂晄姰慡惈掕棟偺徹柧乮敳悎乯乯
丂丂乮俀乯丂僐儞僺儏乕僞乕偺晄姰慡惈丗
丂丂僐儞僺儏乕僞乕偼丄傾儖僑儕僘儉傪昞尰偡傞尵岅乮峔暥榑乯丄傾儖僑儕僘儉傪夝庍偡傞曽朄乮堄枴榑乯丄夝庍偟偨傾儖僑儕僘儉傪強掕偺庤弴偱幚峴偡傞曽朄乮儅僔儞壔乯偺掕幃壔偵傛偭偰峔惉偝傟傞丅峔暥榑偲堄枴榑偼 弎岅榑棟偺岞棟宯偲摨偠傛偆偵尩枾偵掕媊偱偒傞偺偱丄僥儏乕儕儞僌偼傾儖僑儕僘儉偺奺僗僥僢僾傪弎岅榑棟偵傛偭偰悇榑婯懃壔偟丄弮悎偵婡夿揑側憖嶌偵傛偭偰摎傪摫偔儅僔儞乮僥儏乕儕儞僌丒儅僔儞乯傪憐掕偟偨乮1936乯丅
丂丂尰戙偺僐儞僺儏乕僞乕偱偼丄摿掕尵岅偺僾儘僌儔儉偵傛偭偰丄傾儖僑儕僘儉偑僜僼僩僂僃傾偲偟偰僴乕僪僂僃傾偺奺憰抲偵慻傒崬傑傟傞傛偆偵側偭偰偄傞丅 偨偲偊偽丄俛俙俽俬俠尵岅偱偼丄
丂丂丂丂丂丂丂丂丂丂丂丂
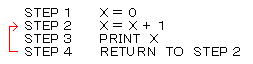
丂丂僾儘僌儔儉偺婰崋偼丄侾屄偺婰壇夞楬 倃 偵 亖 偺塃曈偺抣傪忋彂偒偡傞柦椷傪昞偟丄寢壥偼丄乭侾丄俀丄俁丄丒丒丒乭偑僾儕儞僩偝傟傞丅俽俿俤俹 係偐傜俽俿俤俹 俀 傊栠傞柦椷偼乭儖乕僾乭偲屇偽傟丄偙傟傪悢妛揑偵昞尰偡傞偲 僎乕僨儖偺乭尨巒婣擺娭悢乭偱偁傞丅
丂丂偝偰丄偙偺僥儏乕儕儞僌丒儅僔儞偼丄帺慠悢榑傪娷傓堦斒僔僗僥儉偱偁傝丄晄姰慡惈掕棟偑奼挘偝傟偰丄師偺掕棟偑摫偐傟傞丅偙傟傜偼偄偢傟傕 傾儖僑儕僘儉偵傛傞巚嶕偺尷奅丄偡側傢偪丄僐儞僺儏乕僞乕偺棟榑揑側尷奅傪帵偟偰偄傞丅
丂丂僎乕僨儖丒僥儏乕儕儞僌偺晄姰慡惈掕棟丗丂偡傋偰偺恀棟傪徹柧偡傞僥儏乕儕儞僌丒儅僔儞乮亖 僐儞僺儏乕僞乕乯偼懚嵼偟側偄丅乮1936乯
丂丂僠儍乕僠偺旕寛掕惈掕棟丗丂擟堄偺僥儏乕儕儞僌丒儅僔儞偑壗傪摫偔偐傪帠慜偵寛掕偡傞傾儖僑儕僘儉偼懚嵼偟側偄丅
丂丂僥儏乕儕儞僌偺掆巭掕棟丗丂擟堄偺僥儏乕儕儞僌丒儅僔儞偑偄偮掆巭偡傞偐傪帠慜偵寛掕偡傞傾儖僑儕僘儉偼懚嵼偟側偄丅
丂丂丂丒丒丒丂僐儞僺儏乕僞乕偵庣傜傟偨乭僶儀儖偺搩乭偼偳傫側偵姰慡偵嶌偭偰傕晄姰慡偱偁傞丅俇俇俇偺徾挜乮栙侾俁丗侾俉丄憂侾侾丗係乯丅丂戞俇擔偵憿傜傟偨乭廱乭偲乭恖娫乭乮憂侾丗俀俇乯偼偁傜備傞曽柺偱 恄偺埨懅乮乭俈乭乯偵払偟摼側偄両
丂丂乮俁乯丂恖娫婡夿榑偺斲掕偵偮偄偰乮枹夝寛乯丗
丂丂昐悢廫壄屄偁傞恖娫偺擼嵶朎偺廤崌懱偑偡傋偰偺惛恄妶摦丒棟惈傪寛傔傞偺偩傠偆偐丠 僯儏乕儘儞堦偮堦偮偵揹嬌傪巋偟 偦偺婡擻傪挷傋傞尋媶偼抂弿偵偮偄偨偽偐傝偱偁傞偑丄僯儏乕儘儞偑乭俷俶忬懺乮敪壩忬懺乯乭偐乭俷俥俥忬懺乭偺偄偢傟偐偺忬懺傪偲傞偙偲偼丄僨僕僞儖怣崋偺乭侽乭丄乭侾乭 偲摨偠偱偁傞偲偄偆偙偲偑抦傜傟偰偄傞丅偙傟偼丄丄恖娫偺惛恄峔憿偑彮側偔偲傕僐儞僺儏乕僞乕偺懁柺偑偁傞壜擻惈傪帵嵈偟偰偄傞丅
丂丂 偟偐偟丄弮悎偵榑棟妛揑庤朄偵傛偭偰丄晄姰慡惈掕棟偐傜 僎乕僨儖偼乭恖娫婡夿榑乭偺斲掕傪帵偦偆偲偟偨丅
丂丂僾儘僌儔儉偺儖乕僾偵憡摉偡傞尨巒婣擺娭悢偼堦斒婣擺娭悢偵奼挘偝傟丄傑偨丄巚嶕偵傛傞堦斒揑側乭寁嶼壜擻惈乭偼丄乭僥儏乕儕儞僌丒儅僔儞偺寁嶼壜擻惈乭偲摨摍偱偁傞偙偲偑徹柧偝傟偨丅乮僠儍乕僠乚僥儏乕儕儞僌偺採彞乯乮1937乯
丂丂偟偨偑偭偰丄傾儖僑儕僘儉偱昞尰偱偒傞偡傋偰偺乭巚嶕乭偼 僐儞僺儏乕僞乕偺寁嶼壜擻惈偲摨偠偱偁傞丅偙偙偱丄傕偟丄恖娫偺巚嶕偑傾儖僑儕僘儉偵婎偯偄偰婡擻偡傞側傜偽丄彮側偔偲傕棟惈偵偁偭偰丄恖娫偼僐儞僺儏乕僞乕偲摨偠偙偲偵側傞丅乮恖娫婡夿榑乯
丂丂僎乕僨儖偑摫偄偨斀婡夿榑偼丄悢妛幚嵼榑偲僙僢僩偺宍偱摫弌偝傟丄俀抜奒偺乭慖尵柦戣乭偺宍偱偁傞丅乮1951丄僊僽僘島墘乯
丂丂掕媊侾丂偡傋偰偺乭恀偺乭悢妛揑柦戣偺懱宯傪乭媞娤揑悢妛乭偲屇傇丅
丂丂掕媊俀丂偡傋偰偺乭徹柧壜擻側乭悢妛揑柦戣偺懱宯傪乭庡娤揑悢妛乭偲屇傇丅
丂丂婣寢侾丂悢妛偑媞娤揑悢妛側傜偽丄偄偐側傞岞棟宯傕偡傋偰偺悢妛傪娷傒偊側偄丅乮晄姰慡惈掕棟偲摨偠乯
丂丂婣寢俀丂悢妛偑庡娤揑悢妛側傜偽丄恖娫偼桳尷婡夿偲摨偠偱偁傞丅乮婡夿榑乯
丂丂丒丒丒丂婣寢俀偼 晄姰慡惈掕棟傛傝丄恖娫惛恄傕 僐儞僺儏乕僞乕摨條 帺屓偺晄姰慡惈偵捈柺偟丄恖娫惛恄偺婡擻傪姰慡偵偼棟夝偟偊側偄偙偲偵側傞丅傕偟丄婣寢俀傪斲掕偡傞偲師偺婣寢偑摫偐傟傞丅
丂丂婣寢俁丂恖娫惛恄偼丄偄偐側傞桳尷婡夿傪傕忋夞傞丅
丂丂婣寢係丂恖娫惛恄偵傛偭偰丄愨懳揑偵寛掕晄壜擻側懡崁幃栤戣乮亖 僎乕僨儖柦戣乯偑懚嵼偡傞丅
丂丂慖尵俙丂婣寢俁丄傑偨偼丄婣寢係丄傑偨偼丄偦偺椉曽偑惓偟偄丅
丂丂丒丒丒丂婣寢俁偺傒偑惓偟偄偲偡傞偲丄師偺婣寢偑摫偐傟傞丅
丂丂乮乮拲乯丂僎乕僨儖偼屻偵婣寢係傪斲掕偟偨偑丄偙傟偼斵偺娫堘偭偨乭怣擮乭乮亖崌棟庡媊揑悽奅娤乯偵傛傞傕偺偱偁傝丄偙偺屄強偺斵偺榑朄偼屆揟榑棟偐傜偡傞偲乭榑揰愭庢傝偺嫊婾乭偵側偭偰偄傞丅乯
丂丂婣寢俆丂恖娫惛恄偼丄擼偺婡擻偵娨尦偱偒側偄丅乮斀婡夿榑乯
丂丂婣寢俇丂悢妛揑懳徾偼丄恖娫惛恄偐傜撈棫偟偰懚嵼偡傞丅乮悢妛揑幚嵼榑乯
丂丂慖尵俛丂婣寢俆丄傑偨偼丄婣寢俇丄傑偨偼丄偦偺椉曽偑惓偟偄丅
丂丂丒丒丒丂悢妛揑幚嵼榑偼丄悢妛偑恖娫惛恄偲撈棫偟偰懚嵼偟偰偄傞偙偲偱偁傝丄尰嵼偙傟傪巟帩偟偰偄傞悢妛幰丄揘妛幰偼懡偄丅偙偺傛偆偵丄尰嵼偺偲偙傠丄恖娫偑扨側傞婡夿埲忋偺懚嵼偱偁傞偙偲偺壜擻惈偑榑偠傜傟偰偄傞丅
丂丂偙傟傜偺峫嶡偼偁傞庬偺乭惗婥榑乭傪巟帩偟偰偄傞傛偆偵尒偊傞丅偡側傢偪丄恖偼丄尵梩傗弎岅榑棟傪梡偄傞乭棟惈揑乭側惗暔偱偁傞偲摨帪偵丄杮棃乭楈揑乭側懚嵼偱偁傞丅
丂丂乽偦偺屻丄恄偱偁傞庡偼丄搚抧偺偪傝偱恖傪宍憿傝乮婡夿榑乯丄偦偺旲偵偄偺偪偺懅傪悂偒崬傑傟偨乮惗婥榑乯丅偦偙偱丄恖偼丄惗偒傕偺偲側偭偨丅乿乮憂俀丗俈乯
丂丂乮係乯丂堚揱巕偵傛傞敪惗夁掱偺晄姰慡惈乮僠儍僀僥傿儞乮仏仏乯偺儔儞僟儉惈乯丗
丂丂戝偒側帺慠悢偺寘偵尰傟傞偦傟偧傟偺悢乮俀恑悢乯偵偮偄偰丄偨偲偊偽丄
丂丂100100100100100100100100丂偼丂100 偺俉夞偺孞傝曉偟丄偲抁偔昞尰偱偒傞乮埑弅壜擻乯偑丄
丂丂101100010111010011011010丂偼丂偙傟埲忋偺婯懃惈傪尒弌偣側偄乮埑弅晄壜擻乯丅
丂丂屻幰偺傛偆偵丄乭偦傟帺恎傛傝傕埑弅偱偒側偄悢楍乭傪 乭儔儞僟儉乭偲 悢妛揑偵掕媊偡傞偙偲偑偱偒傞丅
丂丂帺慠悢榑傪娷傓僔僗僥儉 俽 偺丄岞棟偲悇榑婯懃傪婰弎偡傞僾儘僌儔儉傪丄俀恑朄偱僐乕僪壔偟偨價僢僩悢傪 値 偲偡傞丅 傕偟丄俽 偑 値 價僢僩傛傝傕挿偄悢楍偺儔儞僟儉惈傪徹柧偱偒傞側傜偽丄偦偺徹柧傪壜擻偵偡傞 値 價僢僩埲撪偺僒僽僾儘僌儔儉偑懚嵼偡傞偼偢偱偁傞丅偟偐偟丄儔儞僟儉惈偺掕媊偵傛傝丄値 價僢僩傛傝傕挿偄儔儞僟儉悢偼 偦傟傛傝傕埑弅偝傟偨僾儘僌儔儉偱偼昞尰晄壜擻偱偁傝丄偙傟偼柕弬偱偁傞丅偟偨偑偭偰丄
丂丂僎乕僨儖丒僠儍僀僥傿儞偺晄姰慡惈掕棟丗丂擟堄偺僔僗僥儉 俽 偵偍偄偰丄偦偺儔儞僟儉惈傪徹柧晄壜擻側儔儞僟儉悢 俧 偑懚嵼偡傞丅乮1987丄僠儍僀僥傿儞丒俬俛俵儚僩僜儞尋乯
丂丂丒丒丒丂儔儞僟儉悢 俧 偼僎乕僨儖柦戣偺堦偮偱偁傞丅懡崁曽掱幃偺夝偑桳尷偐柍尷偐傪寛掕偡傞偨傔偺 柍尷偵懕偔柦戣偲摨條偱偁傞丅
丂丂儔儞僟儉偵慖戰偝傟偨僾儘僌儔儉偑丄僐儞僺儏乕僞乕偱摦偐偝傟偨応崌偵 掆巭偡傞妋棪 兌 傪掕媊偡傞丅乮兌 亖 侽 偺偲偒 偡傋偰偺僾儘僌儔儉偑掆巭偟側偄丄 兌 亖 侾 偺偲偒 偡傋偰偺僾儘僌儔儉偑掆巭偡傞丅捠忢偼 侽 偲 侾 偲偺娫偵偁傞丅乯
丂丂岞棟宯 俽 偲柦戣 俹 傪婰弎偡傞偨傔偵 値 價僢僩昁梫偱偁傞偲偡傞偲丄岞棟宯 俽 偵傛偭偰 柦戣 俹 偼乭徹柧壜擻乭乮偁傞偄偼乭斀徹壜擻乭乯偱偁傞 偲偄偆偙偲偼丄乭僾儘僌儔儉偑掆巭偡傞乭 偲偄偆偙偲偲摨抣偱偁傞丅
丂丂乮寛掕晄壜擻偱偁傟偽柦戣偼偄偮傑偱傕偩傜偩傜懕偒 掆巭偟側偄丅寁嶼帪娫偺挿偝偱偼側偔丄寁嶼夁掱偺僾儘僌儔儉偺暋嶨偝偵傛傞丅乯丂偡側傢偪丄僾儘僌儔儉偺掆巭妋棪 兌 偼丄岞棟宯 俽 偵傛傞擟堄偺柦戣 俹 偺乭恀棟惈乭傪昞偟偰偄傞丅
丂丂偲偙傠偑丄忋婰偺 僥儏乕儕儞僌偺掆巭掕棟偵傛傝丄僠儍僀僥傿儞偼 偙偺恀棟惈 兌 偑姰慡偵儔儞僟儉偱偁傞偙偲傪徹柧偟偨丅
丂丂僠儍僀僥傿儞偺掕棟丗丂恀棟惈 兌 偼丄儔儞僟儉偱偁傞丅
丂丂僔僗僥儉 俽 偵偍偗傞擟堄偵慖偽傟偨柦戣 俹 偺恀婾惈偼丄忋婰偺悢楍 1011000101丒丒丒 偺傛偆偵弮悎偵儔儞僟儉偱偁傞丅偁傜備傞僾儘僌儔儉偑掆巭偡傞偐偟側偄偐偼丄僐僀儞搳偘偵傛傞悢楍偲丄悢妛揑偵偼壗偺曄傢傝傕側偄丅棟惈偩偗偱敾抐偡傞側傜偽丄恄偼丄暔棟妛偵偍偄偰偺傒偱偼側偔丄悢妛偵偍偄偰傕乭僒僀僐儘傪怳傞乭偺偱偁傞両
丂丂偟偨偑偭偰丄僔僗僥儉偼帺屓偺忣曬検乮暋嶨偝乯傪挻偊偨儔儞僟儉惈傪寛掕偱偒側偄丅偡側傢偪丄帺屓僾儘僌儔儉傪姰慡偵棟夝偡傞僐儞僺儏乕僞乕偺奣擮偼晄壜擻偱偁傞丅
丂丂偙偺偙偲傪丄堚揱巕偵傛偭偰惗暔偑敪惗偡傞夁掱偵揔梡偡傞偙偲偑偱偒傞丅
丂丂俢俶俙偵偁傞乭堚揱巕忣曬乭傪 惗柦懱傪峔惉偟嶌傝忋偘傞偨傔偺乭僾儘僌儔儉乭偲夝庍偡傞側傜偽丄偦偺弌棃忋偑偭偨惗壔妛揑僐儞僺儏乕僞乕偺乭暋嶨惈乭偼丄 兌 偺娷傓忣曬撪梕偲摨偠掱搙偵偟偐寁傟側偄丅傾儖僑儕僘儉偑偦傟埲忋暋嶨偵惉挿偡傞偲丄尨棟揑偵丄堚揱巕夁掱偺摿掕偑晄壜擻偵側傞丅
丂丂乮捈宎俁侽cm偺偍壔偗僔僕儈丄嫲棾偺嫄戝壔偺堚揱巕偱偼側偔娐嫬偵傛傞尷奅丠乯
丂丂乽栭偼怮偰丄挬偼婲偒丄偦偆偙偆偟偰偄傞偆偪偵丄庬偼夎傪弌偟偰堢偪傑偡丅偳偺傛偆偵偟偰偐丄恖偼抦傝傑偣傫丅乿乮儅僐係丗俀俈乯
丂丂丒丒丒丂傒偙偲偽偺庬偺惉挿偲摨偠丅 椙偄敒偲撆敒偲偼惉挿搑拞偱尒暘偗傜傟側偄丅幚傪寢傫偱偄傞偐偺寢壥傪尒偰宱尡揑偵抦傞偟偐側偄丅