４．　 物理化学の ｅ ：



　同じような物がたくさん集まると、その全体の（マクロの）挙動はどのようになるでしょう？　全宇宙の物質は、原子、分子、イオン、電子などの素粒子のように、同じような物が非常にたくさん集まって作られています。　自然対数の底 ｅ は、ミクロとマクロの接点に現われ、”砂粒の集合体”のすべての理論に用いられています。
　統計学や統計力学、熱力学、物理化学の分野では、多くの場合、ｅ のみ現れ、π、ｉ は出現しません（＊１）。　したがって、これらは神の根源性の重要な部分を欠く理論であり、いわば、”死”としての ｅ を扱う理論です。

　もちろん、工学的には非常に重要で、我々が直感的に理解しやすい便宜上のみかけの変数（温度Ｔ、濃度ｃ、圧力ｐ、エントロピーＳ、電気伝導度σ（＝電気抵抗 Ｒの逆数）など）が ｅ の関数に含まれ、頻繁に用いられます。工学とは、いかに資源を効率良く用いて人工的な製品を作るかの、”消費の理論”です。
　（ただし、電磁場、固体の振動に関わる物性論では、時間 ｔ の関数として一部π、ｉ が現れ、空間の広がりを対象とする分子運動論などではπが現れます。）

　また、古典物理は、量子力学のための”予型”となる位置付けとなります。解析力学で構築された数式の形は、量子力学でもそのまま用いられ、しかもそれが本質的な意味を持ちます（＊２）。
　それはちょうど、律法やいろいろな儀式の規定を定めた不完全な契約の旧約時代（古い、暫定のｅ）では終わらず、それらの”実体”である御子イエス様による救いの完全な契約の新約時代（新しい、本質的なｅ）へ変化したようです。

　　（＊１　　量子力学は、物質波の概念にｅ、π、ｉ が密接に関連し、それゆえ神のご性質に関わる根源的な理論であると言えます。
　　　＊２　　単なる確率から本質的な意味を持つ波動関数への変化。ユダヤ人であるアインシュタインは、この量子論の解釈問題でつまづき、その本質的な意味をどうしても納得できなかったのは非常に象徴的で興味深い。）



　（１）　熱力学から出発する場合の ｅ の出所：


　ｄＵ ＝ ＴｄＳ − ＰｄＶ （熱力学の第１法則、ただし、Ｕ　系の内部エネルギー、Ｔ　絶対温度（摂氏温度＋273．15）、　Ｓ　エントロピー、Ｐ　圧力、Ｖ　体積）は、我々の日常感覚の経験則（ボイル・シャルルの法則）からまとめられました。これを用いて、たとえば、閉じた系の理想気体のエントロピー変化�凾rを計算すると、

　　　


　ここで、１次微分 ｄＴ/Ｔ、ｄＶ/Ｖの積分から、自然対数の底 ｅ が出現します。　この出方は、前述のファラデーの法則を Ｖ＝Ｒ ｉ によって変形した ｄＶ/Ｖ（Ｖは電圧）の積分と同じです。これは”法則”という名の”人間の直感”がある程度、神の思索に似ている事をあかししていますが、熱力学においては決して２次以上になる事（π、ｉ も現れる事）はありません。
　エントロピーＳは、下記の統計的考察から、構成粒子の配列の乱雑さの度合いを表します。内部エネルギーのうちのＴＳは、閉じた系においてもはや力学的に利用できない熱エネルギー成分であり、それが最大になるとき、いわば”熱的な死”を意味します。



　（２）　化学平衡論の ｅ


　反応が平衡に達するということは、その系のエントロピーが最大になるという事、すなわち、取り出し得る力学的エネルギーが無くなって完全に死んだ状態です。
　この状態で、化学反応に有効に働くエネルギー成分として、Ｇ（ギブズの自由エネルギー）を、Ｇ ≡ Ｕ＋ＰＶ−ＴＳ （＝ Ｈ−ＴＳ）と定義すると、微小変化 ｄＧ＝ＶｄＰ−ＳｄＴは、温度Ｔ＝ｃｏｎｓｔ（一定）とすればＳｄＴの項が消え、Ｖ＝ＲＴ/Ｐより、上と同様に 1/P の積分となり、各温度についての圧力または濃度の自然対数の形になります。

　　　　∴　�凾f ＝ −ＲＴ ｌｎ ｘ ｉ 、または、＝ −ＲＴ ｌｎ ａｉ 、＝ −ＲＴ ｌｎ Ｐｉ 、などそれぞれの場合について成立
　　　　　　　　　　　　　　ただし、　ｘ ｉ ：成分 ｉ の　モル分率（濃度）、　ａｉ ：活量（有効に働く濃度）、 　Ｐｉ ：分圧

　したがって、一般的な化学反応　　ν１Ａ１　＋　ν２Ａ２　＋　・・・・　→　ν１’Ａ１’　＋　ν２’Ａ２’　＋　・・・・　　において、　平衡定数 Ｋｐ（Ｔ）が次のように与えられます。

　　　　　　　　　　　　　　
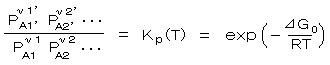
　Ｋｐは反応がどのくらいの割合で平衡に達するかを決める定数で、指数的に温度Ｔと�凾fに依存します。　�凾f0 は標準生成ギブズの自由エネルギーと呼ばれ、２５℃における物質１ｍｏｌを成分元素の単体から作る際要するエネルギーで、反応がどちら方向へどのくらい進むかの駆動力の目安になります。


　実例として、高炉（溶鉱炉）におけるガスとの反応を挙げると、高炉の中の諸反応のうち最も重要な反応は、
　　　　　　　　　　　　　　　　Ｆｅ0.95Ｏ ＋ ＣＯ ＝ 0.95Ｆｅ ＋ ＣＯ2　　　であり、
　ガス分圧との平衡は、　　　ｌｏｇ（ＰＣＯ2/ＰＣＯ） ＝ −�凾g298/4.575Ｔ ＋ �凾r/4.575　　で表される。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（�凾f＝�凾g−Ｔ�凾rより）
　この�凾g（生成エンタルピー）、�凾r（生成エントロピー）に実測値（ｃａｌ/ｍｏｌ）を代入すれば、
　　　　　　　　　　　　　　　　　　ｌｏｇ（ＰＣＯ2/ＰＣＯ） ＝ 800/Ｔ − 0.66　　
　　　　　　　　　例えば、Ｔ ＝ 1000 Ｋで、　ＰＣＯ2/ＰＣＯ ＝ １．３８、すなわち、４２％ＣＯ、５８％ＣＯ2 となる。

　ｌｏｇ（ＰＣＯ2/ＰＣＯ）と１/Ｔとのグラフを書けば直線になり、実験値のプロットにより係数を推定する事ができ、これは工学的によく用いられる手法です。

　半導体中の伝導電子の濃度についても全く同様です。
　　　



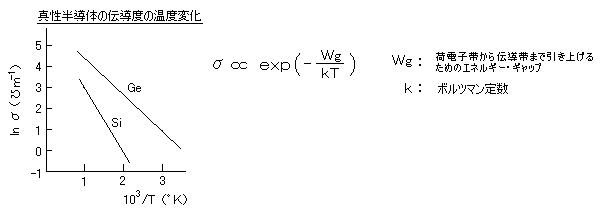
　（３）　統計力学から出発する場合の ｅ の出所：


　個別的な各粒子の取り得る定常状態のエネルギーが、たとえば量子論的に（＊３）不連続な値　ε1、ε2、ε3、・・・　となっていて、それぞれに、Ｎ1個、Ｎ2個、Ｎ3個、・・・　の粒子が割り当てられる場合の数は、

　　　　　　　　　　

　この Ｗ（微視的状態数）が最大になる状態が、熱力学的な平衡状態です。この時の ｌｎ Ｗ の極値を定めるために、
　　　　　　　スターリングの近似式　　ｌｎ Ｎ！ ＝ Ｎ ｌｎ Ｎ − Ｎ　　（ただし、Ｎは非常に大きい数）
　を用いて展開し、次の関係諸式が得られます。

　　　

　式（1）、（4）、（5）は、熱力学（マクロ）と統計力学（ミクロ）を結びつける重要な関係式です。　特に、（5）はボルツマンの式と呼ばれ、エントロピーの分子論的な意味を理解させる式であり、熱力学の第２法則（エントロピー増大則）を説明します。すなわち、微視的状態数 Ｗ が大きいほど実現確率が高く、孤立系、断熱系（Ｅ、Ｎ一定）では、Ｗ が最大になる状態が、熱力学的平衡状態に対応します。
　また、ネルンストによる熱力学の第３法則は、絶対零度（０ Ｋ）では、純粋物質の完全結晶はエントロピーが０ですが、この時の微視的状態は、Ｗ0 ＝ Ｎ！/Ｎ1！、　Ｎ ＝ Ｎ1　より、Ｗ0 ＝ １、したがって、（5）は、　Ｓ ＝ ｋ ｌｎ １ ＝ ０ となります。
　ここで、（1）〜（3）の指数関数 も、（5）の自然対数 ｌｎ も、平衡状態（充分死んだ状態）において、スターリングの近似式（＊４）から出たものです。
　このように、ミクロとマクロの接点に ｅ が存在し、直感できないミクロの状態を、ｅ によって、我々の直感できるマクロのいろいろな変数に直しているのです。

　　（＊３　古典論的な、すなわち、系が連続のエネルギー値をとる場合も、一般力学のハミルトン関数 Ｈ を用いて、全く同様の結果が得られるが、不連続値から始めたほうが理解しやすい。
　　＊４　スターリングの近似式を証明する事は高度な数学を必要とし難解なので省略する。　）



　気体分子運動論による速度分布の形は、正規分布（ガウス型分布）になります。ここにも、変則的な ｅ が出現しています。
　　


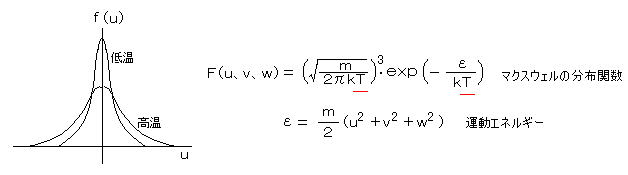
　「御子をさえ惜しまずに与えてくださった方が、どうして御子といっしょに全てのものを与えないだろうか」（ロマ９：３２）

　神様は”豊かに、惜しみなく与える神”、「エル・シャダイ（＝乳房の神）」です。これは神様の母親的要素をあかしする名前です。私たちは、神様が創造の初めに造られたあらゆる資源を消費して生かされています。地下資源などを利用していますが、私たちの体を成り立たせる生物のエネルギーに関しては、実に、はるか遠くにある太陽の中心部の核融合反応からの光によって全面的にまかなわれています。ただし、宇宙全体のエントロピーは確実に増加しつつあり、二度と元に戻る事はありません。これは、輪廻ではなく、創造の”初め”が存在した事の重要なあかしです。
　金属精錬の祖、トバル・カインに職を与えた神様は恵みとあわれみの神です。そして、資源を消費する時も、ｅ （イエス様）が現れます。

　

　　　　　　　　　　　　　　　　　　　　　　　　　次へ