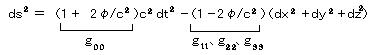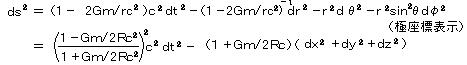丂丂丂丂丂丂丂丂憡懳惈棟榑偺徻嵶
丂侾丏丂摿庩憡懳惈棟榑偺尨棟丟
丂丂丂丂丂丂丂丂懍搙堦掕偺擟堄偺宯乮姷惈宯乯偵偍偄偰丄
丂丂丂丂丂乮1乯丂偦偙偐傜娤應偝傟傞恀嬻拞偺岝懍 c 偼堦掕
丂丂丂丂丂乮2乯丂偦偺宯偺偡傋偰偺暔棟朄懃偼摨條偵惉傝棫偮
丂俀丏丂摿庩憡懳惈棟榑偺揥奐丟
丂1乯丂儘儗儞僣曄姺丟
丂娤應幰偑俽宯偵偄偰丄旐娤應検偑俽乫宯偵偁傝丄俽乫宯偼俽宯偵懳偟偰 亄 倶曽岦偵懍搙
倴 偱摦偄偰偄傞偲偡傞丅
丂俽乫宯偱丂倶乫=0丂偺揰偼 俽宯偐傜尒傟偽丂倶 = 倴倲丂丄丂俽乫宯偱丂倶乫=-倴倲乫丂偺揰偼
俽宯偐傜尒傟偽丂倶=0丂偵側傞偺偱丄
丂丂丂丂丂丂丂倶乫 = 0 = 兝乮倶 亅 倴倲乯
丂丂丂丂丂丂丂倶 = 0 = 兞乮倶乫亄 倴倲乫乯
丂偲抲偗傞丅
丂偙偺幃傛傝丄倶乫=兝乮倶亅倴倲乯丄倲乫=乮倶亅兞倶乫乯/倴 = 乮乮1亅兝兞乯倶亄兝兞倴
倲乯/倴 傪丄帪嬻偺惈幙
丂丂丂丂丂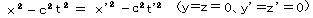
偵戙擖偟偰丄
丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丂乮嵗昗娫偺曄姺懃乯
丂偟偨偑偭偰丄俽乫宯偵屌掕偟偨倃幉偵暯峴偺朹偺挿偝 俴0亖 倃2乫亅倃1乫偼丄俽宯偐傜尒偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂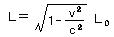 丂偺傛偆偵抁偔尒偊傞丅
丂偺傛偆偵抁偔尒偊傞丅
丂傑偨丄俽宯忋偱丂倃0偵抲偄偨帪寁偑丂俿1丄俿2丂傪偝偟偨帪丄俽乫宯偱偼丂俿1乫丄俿2乫傪偝偟偰偄傞偐傜丄俽乫宯偺傕偺偼丂俽宯偺傕偺偵斾傋丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂攞傕帪娫傪宱傞傛偆偵尒偊傞丅
丂攞傕帪娫傪宱傞傛偆偵尒偊傞丅
丂丂丂丂乮仏丂崌惉懍搙偺掕棟丄幙検偺儘儗儞僣曄姺丄揹帴応偺儘儗儞僣曄姺丄揹帴攇曽掱幃偺儘儗儞僣晄曄惈側偳偼徣棯乯
丂2乯丂幙検岞幃丟
丂俽宯乮娤應宯乯偵偍偗傞懍搙偼堦掕偲偼偐偓傜偢俽宯忋偺帪娫 t 偵傛傞傕偺偲偡傞偲丄懍搙儀僋僩儖偼丄
丂丂丂丂丂丂丂丂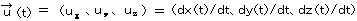
丂儘儗儞僣曄姺偼丂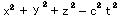 丂偑晄曄側曄姺偱偁傞偐傜丄
丂偑晄曄側曄姺偱偁傞偐傜丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂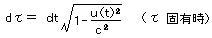 丂偲偍偗偽丄冄偼儘儗儞僣晄曄乮徹柧棯乯丅
丂偲偍偗偽丄冄偼儘儗儞僣晄曄乮徹柧棯乯丅
丂係尦懍搙丗丂
丂丂丂丂丂丂
丂偺傛偆偵掕媊偡傞偲丄
丂丂丂丂丂丂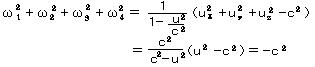
丂椉曈傪冄偱旝暘偡傟偽丄
丂丂丂丂丂丂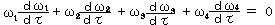
丂椉曈傪倣0攞偟偰4尦懍搙偺幃傪戙擖偡傟偽丄
丂丂丂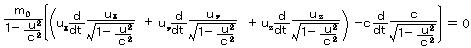
丂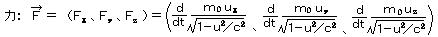 偲抲偗偽丄
偲抲偗偽丄
丂丂丂丂丂丂丂丂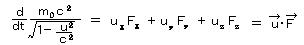
丂倲丂偱旝暘偡傟偽丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂倳 亖 0丂偺帪丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂乮惷巭幙検偺僄僱儖僊亅乯
丂乮惷巭幙検偺僄僱儖僊亅乯
丂俁丏丂堦斒憡懳惈棟榑偍傛傃廳椡棟榑丟
丂1乯丂摍壙尨棟丟
丂廳椡偲姷惈椡偺摍壙傪壖掕偡傞傕偺偱丄僯儏亅僩儞椡妛偵偍偗傞愨懳帪嬻拞偺廳椡偱偼側偔丄廳椡傪嬋偑偭偨儕乕儅儞嬻娫偵偍偗傞寁検僥儞僜儖乮10屄偺倗倝倠丄倝丄倠=1乣4乯偵庢傝崬傫偱丄嶰師尦偲帪娫偺係尦僷儔儊亅僞偵傛偭偰婔壗妛揑偵昞尰偡傞傕偺偱偁傞丅
丂2乯丂傾僀儞僔儏僞僀儞偺廳椡応偺曽掱幃丟
丂廳椡応冇偺億傾僜儞幃丂仮冇亖亅係兾俧兿丂乮仮丒丒丒儔僾儔僔傾儞乯偵傛傞昞尰偺堦斒壔傪峴側偆偲丄
丂丂丂丂丂丂丂丂丂丂丂丂 丂丂
丂丂
丂俿倝倠偼暔幙暘晍偲僄僱儖僊亅暘晍偱寛傑傞検偱偁傞丅
丂3乯丂廳椡曽掱幃偺夝丟
丂傾僀儞僔儏僞僀儞偺廳椡曽掱幃偼憡懳榑偺尋媶幰傜偵傛偭偰偄偔偮偐偺夝偑梌偊傜傟偨丅
丂鶣乯丂庛偄廳椡応偱偺夝乮嬤帡夝乯丟
丂丂丂丂丂丂丂丂丂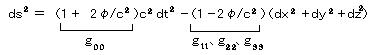
丂偙偺幃偺椺徹偼丄1丏悈惎偺嬤擔揰堏摦乮嚈兤亖 43"/100擭乯丄丂俀丏懢梲廳椡応偵傛傞岝慄偺嬋偑傝乮嚈兤亖
1.75倱倕們乯丄俁丏儊僗僶僂傾乕岠壥偵傛傞抧媴廳椡応偱偺帪娫偺抶傟偺應掕偵傛偭偰梌偊傜傟偨丅
丂鶤乯丂僔儏儚儖僣僔儖僪夝乮尩枾夝乯丟
丂柍尷墦偺娤應幰偵傛傞丄媴懳徧偺幙揰偺傑傢傝偺廳椡応偵懳偡傞傕偺偱丄
丂丂丂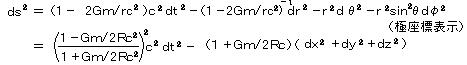
丂乮們倖乯丏儈儞僐僼僗僉乕帪嬻偺摨偠忦審偺幃偲斾傋傞偲學悢偑偳偺傛偆偵曄傢偭偰偄傞偐偑傢偐傞丅
丂丂丂
丂鶥乯丂僇乕夝乮尩枾夝乯丟
丂夞揮傪娷傓夝丅
丂丂丂丂
丂曽掱幃偺夝偺幙揰晅嬤偺條巕偐傜僽儔僢僋儂乕儖偑梊憐偝傟傞丅僔儏儚儖僣僔儖僪偺僽儔僢僋儂乕儖偼丄鶣乯丂俼倱偺奜晹偐傜俼倱偵嬤偯偔偲丄倲
仺 亣丄 岝偺怳摦悢兯仺 0 偵側傞丅
丂丂 鶤乯丂俼倱偺撪晹偺帠偼偁偔傑偱傕悢幃忋偺帠偱丄幚徹晄壜擻丅乮悢幃忋偼丄們倲
偲 倰 偑擖傟懼傢傞乯
丂丂丂丂丂丂丂丂丂丂丂丂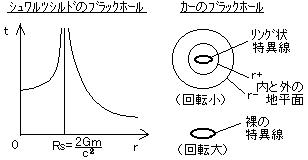
丂鶦乯丂懠偺夝丟
丂丂丂嘆丂僇乕僩丒僎乕僨儖偺夝丟丂旕場壥棩揑夝偱丄帪娫偑儕儞僌忬偵側偭偰偄傞丅
丂丂丂嘇丂俶倀俿夝丟丂崅師尦偱偺傜偣傫宍偺夝偱僞僀儉僩儔儀儖壜擻丠丄暿斉偺帪嬻偺懚嵼丅
丂偙傟傜偼丄棟榑忋偺傕偺偩偗偵夁偓偢丄尰幚偱偼側偄丅乮旝暘曽掱幃側偳偼丄嫬奅忦審偲弶婜忦審偵傛偭偰幚嵺偵偼懚嵼偟側偄夝傪傕嶌傞帠偑偱偒傞惈幙偺傕偺偱偁傞偙偲偵拲堄丅偦偺恖偺巚憐偑惙傝崬傑傟偰偟傑偆応崌偑偁傞丅乯
丂丂丂丂丂丂丂丂丂丂丂栠傞

 丂攞傕帪娫傪宱傞傛偆偵尒偊傞丅
丂攞傕帪娫傪宱傞傛偆偵尒偊傞丅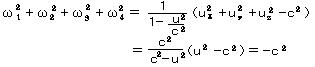

 丂丂
丂丂