丂丂丂丂丂丂丂丂係丏丂晄姰慡惈掕棟乮戞侾掕棟乯偺徹柧
丂丂恄偼丄乭尵梩偺恄乭偱偁傝丄岅偭偨尵梩傪昁偢惉偟悑偘傜傟傞乮僀僓俆俆丗侾侾乯丅 傑偨丄僸僩偺戝擼旂幙偺慜摢梩偵偼丄乭堄巙乭偲嫟偵乭尵岅乭偺拞悤偑偁傝丄偙傟傜偼嫟摨揑偵嶌梡偡傞偺偱丄偙偺偙偲傕丄僸僩偑恄條偵帡偣偰憿傜傟偨旐憿暔偱偁傞偙偲傪偁偐偟偟偰偄傞丅
丂丂偝偰丄偙偺尵梩偲偄偆傕偺傪宍幃揑偵暘愅偡傞偲丄棟惈揑偵昞尰偝傟傞堦斒揑側尵梩偼榑棟妛揑宍幃偵昞尰偱偒丄條憡榑棟乮乣偲怣偠傞丄乣偡傞偩傠偆丄乣偟側偗傟偽側傜側偄丄側偳乯傕娷傔偰丄悢棟榑棟妛揑偵婰崋壔偝傟偡傋偰昞尰偱偒傞傛偆偵側傞丅偦偟偰丄扨弮側丄柦戣榑棟丄弎岅榑棟偼丄恖娫棟惈偐傜尒偰傕姰慡偱偁傞丅
丂丂堦曽丄悢妛揑巚嶕傗奒憌峔憿傪帩偮弎岅榑棟偵偍偄偰偼丄帺屓尵媦傪娷傑側偄丄偨偲偊偽彨婝傗僠僃僗側偳偺僎乕儉偱偼丄偦偺婯懃偑偄偔傜暋嶨偱傕晄姰慡惈偼尰傟側偄偑丄柍尷惈傗帺屓尵媦傪娷傓掱搙偵暋嶨側僔僗僥儉乮帺慠悢榑傪娷傓偡傋偰偺悢妛棟榑偼傕偪傠傫乯偵偍偄偰偼丄塱墦偵寛掕晄擻側僷儔僪僢僋僗偑梕堈偵敪惗偟偆傞偺偱偁傞丅 尵岅偼婰崋偵側傝丄婰崋偼僎乕僨儖悢偵傛偭偰帺慠悢榑偵娨尦偡傞偙偲偑偱偒傞偐傜丄悢妛偺傒側傜偢 奒憌峔憿乮儊僞尵岅乯傪帩偮弎岅榑棟偵偁偭偰傕丄偦偺晄姰慡惈傪乭帺慠悢榑揑側曽朄乭偵傛偭偰徹柧偡傞偙偲偑偱偒傞丅
丂丂乮侾乯丂丂宍幃揑帺慠悢榑偺峔憿丗
丂丂戞侾奒偺弎岅榑棟偲偼丄屄懱偵偮偄偰偺傒尷検傪嫋偡榑棟妛偱偁傞丅
丂丂偙偺忋偵峔惉偝傟偨宍幃揑悢妛偼丄戞侾奒偺棟榑偲屇偽傟丄乮弎岅乯榑棟妛偺岞棟偵 悢妛偺岞棟傪捛壛偟偰偮偔傜傟傞丅 乽晄姰慡惈掕棟乿偼丄偙偺乭戞侾奒偺帺慠悢榑乭偱婰弎偡傞偺偑晛捠偱偁傞丅偦傟偼丄偙偺戞侾奒偺棟榑偼丄幚悢榑傗廤崌榑偺奣擮傪慡偔娷傑側偄偱峔惉偝傟偰偄傞偐傜偱偁傞丅
丂丂偙傟傜偼丄師偺傛偆側庤弴偱峴傢傟傞丅
丂丂丂丂丂丂丂棟榑丂丂仺丂丂宍幃壔乮弎岅榑棟乯丂丂仺丂丂弎岅榑棟偺乽姰慡惈乿偺徹柧
丂丂丂丂丂丂丂棟榑丂丂仺丂丂宍幃壔乮弎岅榑棟乯亄悢妛揑岞棟宯丂丂仺丂丂婣擺揑弎岅偲婣擺揑娭悢偺愝掕
丂丂丂丂仺丂丂宍幃揑帺慠悢榑乮儊僞悢妛乯丒僎乕僨儖悢偺掕媊丂丂仺丂丂帺屓尵媦偺摫擖丒僎乕僨儖柦戣偺嶌惉
丂丂丂丂仺丂丂悢妛偺乽晄姰慡惈乿偺徹柧
丂丂侾乯丂丂悢妛揑婣擺朄偺岞棟丟
丂丂桳柤側 儁傾僲嶼弍偺岞棟宯乮1894乯偼師偺傛偆偱偁傞丅
丂丂丂岞棟侾丗丂侽 偼帺慠悢偱偁傞
丂丂丂岞棟俀丗丂倶 偑帺慠悢偱偁傟偽丄倶 偺屻懕悢 倶乫 傕帺慠悢偱偁傞
丂丂丂岞棟俁丗丂侽 偼 偄偐側傞帺慠悢偺屻懕悢偱偼側偄
丂丂丂岞棟係丗丂帺慠悢 倶 偺屻懕悢 倶乫 偲帺慠悢 倷 偺屻懕悢 倷乫偑摍偟偄側傜偽丄倶 偲 倷 傕摍偟偄
丂丂丂岞棟俆丗丂侽 偑偁傞惈幙傪傕偪丄偐偮丄擟堄偺帺慠悢 倶 偑偦偺惈幙傪傕偮側傜偽 倶 偺屻懕悢傕偦偺惈幙傪傕偮丄偙偺偙偲偑尵偊傞偲偒丄偡傋偰偺帺慠悢偼偦偺惈幙傪傕偮
丂丂埲忋偼丄擔忢尵岅傪梡偄偰昞尰偟偨傕偺偱丄乭侽乭丄乭帺慠悢乭丄乭屻懕悢乭偼 乭枹掕媊梡岅乭偲屇偽傟丄偳偺傛偆偵夝庍偡傞偐偼 堄枴榑忋偺栤戣偲側傞丅乮尰戙悢妛偱偼丄倶 偺屻懕悢傪 倶 亄 侾 偲夝庍偡傞偺偑晛捠偱偁傞丅乯
丂丂岞棟 俆 偼丄悢妛揑婣擺朄偺岞棟傪昞偟丄岞棟侾偐傜係傑偱偐傜惗傒弌偝傟傞懳徾偩偗偑帺慠悢偱偁傝丄偦傟埲奜偼帺慠悢偱側偄偲尷掕偡傞傕偺偱傕偁傞丅
丂丂恖岺尵岅乮僞僀僾棟榑乯偱 岞棟 俆 傪婰弎偡傞偲丄
丂丂丂丂丂丂丂丂丂丂佂俹乮俹乮侽乯伻佂倶乮俹乮倶乯仺俹乮倶乫乯乯仺佂倶俹乮倶乯乯丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偨偩偟丄俹丗 帺慠悢偺惈幙傪偁傜傢偡曄崁
丂丂堦曽丄戞侾奒偺棟榑偲偟偰峔惉偝傟偨 帺慠悢榑偺宍幃揑懱宯 俶 偵偮偄偰偼丄
丂丂俶 偺尵岅偼丄偨偩堦偮偺屄懱婰崋 侽 偲丄 俁偮偺娭悢婰崋丂乫 丄亄 丄 丒丂偲丄偨偩堦偮偺弎岅婰崋 亖 傪傕偮丅
丂丂俶 偺悢妛揑岞棟偼丄師偺傛偆偵婰弎偝傟傞丅
丂丂丂俶侾丗丂丂倶乫 亗 侽丂丂丂丂丂丂丂丂丂丂丂丂俶俀丗丂丂倶乫 亖 倷乫 仺 倶 亖 倷丂丂丂丂丂俶俁丗丂丂倶 亄 侽 亖 倶
丂丂丂俶係丗丂丂倶 亄 倷乫 亖 乮倶 亄 倷乯乫丂丂丂 俶俆丗丂丂倶 丒 侽 亖 侽丂丂丂丂丂丂丂丂丂丂俶俇丗丂丂倶 丒 倷乫 亖 倶 丒 倷 亄 倶
丂丂丂俶俈丗丂丂俙乲侽乴 伻 佂倶 乮俙乲倶乴 仺 俙乲倶乫乴乯 仺 佂倶 俙乲倶乴
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偨偩偟丄俙丗丂擟堄偺幃傪昞偡峔暥榑揑曄崁
丂丂俶俈 偑丄悢妛揑婣擺朄偺岞棟偵側偭偰偄傞丅
丂丂儁傾僲偺岞棟俆 偑扨撈偺幃偱昞偝傟偰偄傞偺偵懳偟丄俶俈 偼恾幃偵側偭偰偄傞丅
丂丂戞侾奒偺帺慠悢榑乮偙傟傪丄扨偵丄帺慠悢榑偲屇傇乯偼丄幚悢奣擮傗廤崌奣擮傪娷傑側偄丄嵟傕弶摍揑側帺慠悢榑偺懱宯偱偁傝丄儁傾僲偺帺慠悢榑傛傝傕庛偄懱宯偱偁傞丅
丂丂俀乯丂僎乕僨儖悢偺掕媊丟
丂丂師偺傛偆側婯懃偵傛偭偰丄偁傜備傞弎岅婰崋傪偦傟偧傟堎側傞撈棫偟偨帺慠悢偵悢抣壔偡傞偙偲偑偱偒傞丅偟偨偑偭偰丄媡偵丄偙偺悢抣壔偵傛偭偰丄偁傜備傞尵岅傗悢妛傪帺慠悢榑偺乭婣擺揑側榑朄乭偵曄姺偡傞偙偲偑偱偒傞丅乮偙傟偼丄乮俀乯偺徹柧偱岠壥揑偵梡偄傜傟傞乯
丂丂侾丏丂俶 偺婰崋 倕 偺僎乕僨儖悢丟
丂丂丂
 丂
丂丂丂丂丂丂丂丂丂丂丂丂丂乮乣 偼斲掕丄佂 偼慡徧丄丂乫丂偼 屻幰偺堄乯丂丂俶斣栚偺屄懱曄崁偺僎乕僨儖悢偼丂俀俁亄俀丒乮値亅侾乯
丂丂俀丏丂俶 偺婰崋楍丂丂俤 亖 倕侾 倕俀 丒丒丒丒丒 倕値丂偺僎乕僨儖悢丟
丂丂丂丂丂丂丂丂
丂丂丂婰崋偺僎乕僨儖悢傪 慺悢楍偺檖偵擖傟 偡傋偰妡崌偣傞丅
丂丂丂偨偲偊偽丄幃丂倶 亗 倷丂偡側傢偪丄丂乣亖乮倶丄倷乯丂偺僎乕僨儖悢偼丄
丂丂丂丂丂丂丂丂丂崁丂倶 亄 倸丂偡側傢偪丄丂亄乮倶丄倸乯丂偺僎乕僨儖悢偼丄
丂丂俁丏丂俶 偺婰崋楍偺楍丂俤侾丄俤俀丄丒丒丒丒丒丄俤値丂偺僎乕僨儖悢丟
丂丂丂丂丂丂丂丂丂
丂丂丂偝傜偵丄婰崋楍偺僎乕僨儖悢傪慺悢楍偺檖偵擖傟妡崌偣傞丅
丂丂慺場悢暘夝偺堦堄惈偐傜丄偡傋偰偺婰崋丄婰崋楍丄婰崋楍偺楍偵丄偦傟偧傟堎側傞僎乕僨儖悢偑 侾丗侾 偵懳墳偡傞偺偱丄悢帤偩偗偱偡傋偰偺婰弎傪嬫暿偟偰擣幆偡傞偙偲偑偱偒傞丅 彮側偔偲傕尨棟揑偵偼丄僎乕僨儖悢偑梌偊傜傟傞偲丄傕偲偺婰崋榑棟偵夝撉偱偒傞偙偲偵側傞丅慺悢埫崋偺尨棟丅偨偩偟丄僎乕僨儖悢偼旕忢偵戝偒偄悢偵側傞丅偨偲偊偽丄乭徹柧偺僎乕僨儖悢乭偼 偁傞徹柧偺挿偄婰崋楍傪僎乕僨儖悢壔偡傞偐傜 偍偦傠偟偔戝偒偄悢偵側傞偑丄妋偐偵堦偮偺乭懚嵼偡傞乭帺慠悢偱偁傞丅
丂丂俁乯丂晄姰慡惈偑尰傟傞偟偔傒丗
丂丂帺慠悢榑偼忋壓曽岦偵丄乭柍尷乭偺奣擮傪娷傓丅偙偺柍尷惈傪丄桳尷偺曽朄偱柕弬側偔岞棟宯偵廂傔傞偨傔偵丄儁傾僲偺戞俆岞棟傗戞侾奒偺帺慠悢榑偺 俶俈 偺傛偆側 婣擺揑側掕媊傗婣擺朄偵傛傞徹柧傪摫擖偟側偗傟偽側傜側偐偭偨丅
丂丂偦偺忋偱丄偨偲偊偽 柦戣帺恎偺僎乕僨儖悢傪 偦偺柦戣偺曄悢偵戙擖偡傞偲偄偭偨丄乭帺屓尵媦乭乮偁傞偄偼丄憡屳尵媦乯傪娷傓傛偆偵柦戣傪愝掕偡傞丅偡傞偲丄乭偆偦偮偒偺僷儔僪僢僋僗乭丄乭敳偒懪偪僥僗僩偺僷儔僪僢僋僗乭偲摨條偵丄徹柧傕斀徹傕偱偒側偄寛掕晄擻側柦戣乮僎乕僨儖柦戣乯偑峔惉偝傟傞偺偱偁傞丅偮傑傝丄偦偺悢妛棟榑偼乽晄姰慡乿偲偄偆偙偲偵側傞丅
丂丂乮俀乯丂晄姰慡惈掕棟偺徹柧丗
丂丂偱偼丄幚嵺偵僎乕僨儖偑峴偭偨晄姰慡惈掕棟偺徹柧傪徻偟偔尒偰傒傛偆丅乮懡彮丄婰崋傪娙棯壔偟偰偄傑偡乯
丂丂師偺傛偆側柦戣偑惉棫偡傞丅
丂丂倂乮倶丄倷乯丗丂乽 倶 偼丄堦偮偺帺桼曄崁傪傕偮弎岅 倂倶乮倲乯 偺僎乕僨儖悢偱偁傝丄 倷 偼丄暵弎岅 倂倶乮倶乯 偺徹柧偺僎乕僨儖悢偱偁傞丅乿
丂丂乮偙偺柦戣偑悢榑偺宍幃揑弎岅偱偡傋偰婰弎偡傞偙偲偑偱偒傞偙偲傪帵偡挿偄徹柧偼徣棯偡傞丅偙偺帺慠悢榑偺柦戣 倂 偼丄尨巒婣擺揑乮亖嵞婣揑弎岅偺堦偮乯偱偁傞丅乯
丂丂偙偙偱丄丂丂丂俧乮倲乯 亖 乣佄倷 倂乮倲丄倷乯丂丂丂丂丂丂丂丂丂丂丂乮乮拲乯丂 乣佄倷 倂 偼丄佂倷 乣倂 偲摨偠乯
丂丂丗 乽堦偮偺帺桼曄崁傪傕偮弎岅 倂倲乮倸乯 偺僎乕僨儖悢傪 倲 偲偡傞偲丄偄偐側傞悢 倷 傕 暵弎岅 倂倲乮倲乯 偺徹柧偺僎乕僨儖悢偲偼側傜側偄丅乿
丂丂偲偄偆柦戣傪偮偔傞丅
丂丂偙偺 俧乮倲乯 帺恎傕丄侾曄崁 倲 偺傒傪帺桼曄崁偲偟偰傕偮柦戣偩偐傜丄側傫傜偐偺僎乕僨儖悢 倯 傪傕偮丅乮偡側傢偪丄俧乮倲乯 亖 倂倯乮倲乯 乯
丂丂偙偺摿掕偺掕悢 倯 傪戙擖偟偰摼傜傟傞暵弎岅丄乮仏丂偙偙偵丄乭帺屓尵媦乭傪娷傑偣偰偄傞偙偲偵拲堄両乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俧乮倯乯 亖 乣佄倷 倂乮倯丄倷乯丂丂丂丂丂丂丂丂
丂丂偑丄嘆徹柧傕丄嘇斀徹傕偱偒側偄寛掕晄擻偺乭僎乕僨儖柦戣乭偵側偭偰偄傞偙偲傪帵偡丅乮嘆丄嘇偲傕丄攚棟朄偱徹柧偡傞乯
丂丂嘆丂丂俧乮倯乯 偑徹柧偱偒側偄偙偲偵偮偄偰丟
丂丂傕偟丄俧乮倯乯 偺徹柧偑懚嵼偡傞側傜偽丄
丂丂俧乮倯乯帺恎偺徹柧偺僎乕僨儖悢 倰 偑懚嵼偟偰丄倂乮倶丄倷乯 偺掕媊傛傝丄柦戣 倂乮倯丄倰乯偑惉棫偡傞丅
丂丂傛偭偰丄倂乮倯丄倷乯 傪惉棫偝偣傞 倷 偑懚嵼偡傞偙偲偵側傞丅
丂丂偙偺偙偲偼丄 俧乮倯乯 亖 乣佄倷 倂乮倯丄倷乯丂丄偡側傢偪丄偄偐側傞悢 倷 傕 倂 偺徹柧偺僎乕僨儖悢偵側傜側偄偲偄偆丄偙偺柦戣帺恎偺庡挘偲柕弬偡傞丅
丂丂嘇丂丂俧乮倯乯 偑斀徹偱偒側偄偙偲乮亖 乣俧乮倯乯 偑徹柧偱偒側偄偙偲乯偵偮偄偰丟
丂丂乣俧乮倯乯 亖 佄倷 倂乮倯丄倷乯 偑 恀偱偁傞偲壖掕偡傞側傜偽丄
丂丂嘆傛傝丄 俧乮倯乯 偑徹柧晄擻偱偁傞偙偲偼 恀 偱偁傞偐傜丄偙偙偱丄
丂丂冎柍柕弬丗丂乣俻乮侽乯丄乣俻乮侾乯丄乣俻乮俀乯丄丒丒丒丂偲偄偆柦戣慡懱偲丄佄倷 俻乮倷乯 偲偄偆柦戣偑丄摨帪偵 恀 偲側傞偙偲偼側偄丄丂傪壖掕偡傞偲丄
丂丂倂乮倯丄侽乯丄倂乮倯丄侾乯丄倂乮倯丄俀乯丄丒丒丒丂偼 偡傋偰 婾 偲側偭偰丄偳偺傛偆側帺慠悢傕 偦偺徹柧偺僎乕僨儖悢偵偼側傝摼側偄偲偄偆偙偲偵側傞丅
丂丂偟偨偑偭偰丄丂佄倷 倂乮倯丄倷乯 偼 婾 偲側偭偰丄偙傟偑 恀 偱偁傞偲偄偆壖掕偵斀偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮徹柧廔乯
丂丂嘆丄嘇傪傑偲傔傞偲丄 俶丗 帺慠悢榑偺岞棟宯 乮壜晅斣偱柍尷惈傪傕偪乮亖 婣擺揑偱乯丄帺屓尵媦丒憡屳尵媦傪娷傒偆傞掱搙偵暋嶨側棟榑丒僔僗僥儉側傜偽壗偱傕傛偄乯偲偟偰丄
丂丂嘆丂丂俶 偑柍柕弬偱偁傟偽丄俧 偼 俶 偱徹柧壜擻偱偼側偄
丂丂嘇丂丂俶 偑 冎柍柕弬偱偁傟偽丄乣俧 偼 俶 偱徹柧壜擻偱偼側偄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丒丒丒丂僎乕僨儖偺戞侾晄姰慡惈掕棟乮1931乯
丂丂偙偺 岞棟宯偺 冎柍柕弬偺壖掕偼丄俰丏俛丏儘僢僒乕偵傛偭偰丄
丂丂扨弮柍柕弬丗 佄倷 俻乮倷乯 偲 乣佄倷 俻乮倷乯 偲偼丄摨帪偵恀偲偼側傝摼側偄丄偵奼挘偝傟乮1936乯丄尰嵼丄扨偵乭晄姰慡惈掕棟乭偲屇偽傟傞傕偺偼偙傟傪巜偡丅
丂丂偟偨偑偭偰丄偁傞悢妛棟榑偺岞棟宯偑柍柕弬側傜偽丄偦偺岞棟宯偼晄姰慡丄偡側傢偪丄偦偺暵偠偨棟榑撪晹偱偼徹柧傕斀徹傕偱偒側偄僎乕僨儖柦戣偑懚嵼偡傞偙偲偵側傞丅
丂丂傑偨丄戞俀晄姰慡惈掕棟傛傝丄岞棟宯偑柍柕弬側傜偽丄偦偺岞棟宯帺恎偺柍柕弬惈傪偦偺岞棟宯偐傜徹柧偱偒側偄丅
丂丂丂丒丂戞侾晄姰慡惈掕棟丗
丂丂丂丂丂丂丂嘆丂俶 偑柍柕弬偱偁傞側傜偽丄 俼 偼 俶 偱徹柧壜擻偱偼側偄
丂丂丂丂丂丂丂嘇丂俶 偑柍柕弬偱偁傞側傜偽丄 乣俼 偼 俶 偱徹柧壜擻偱偼側偄
丂丂偙偙偱丄
丂丂丂丂丂丂丂丂丂丂
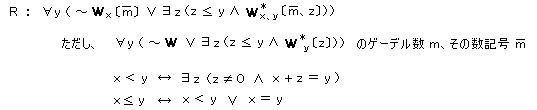
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂悢榑揑弎岅 倂丄倂* 丗丂倂乮倎丄倐乯 佁 俹倖 乮倐丄俽倳倐乮倎丄俀俁丄俶倳倣乮倎乯乯乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂 倂*乮倎丄倐乯 佁 俹倖 乮倐丄俽倳倐乮俀17*倎丄俀俁丄俶倳倣乮倎乯乯乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俽倳倐乮倎丄倐丄們乯丗丂僎乕僨儖悢 倎 偺婰崋楍偺拞偵帺桼曄崁偲偟偰尰傟傞僎乕僨儖悢 倐 偺
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂屄懱曄崁偵丄僎乕僨儖悢 們 偺崁傪戙擖偟偰摼傜傟傞婰崋楍偺僎乕僨儖悢
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂Num乮倎乯丗丂悢婰崋倎-偺僎乕僨儖悢
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倂丄倂* 傪昞尰偡傞幃 倂丄倂*丂偺帺桼曄崁偼偦傟偧傟 倶丄倷 偲偡傞
丂丂丂丒丂戞俀晄姰慡惈掕棟丗
丂丂丂丂丂丂丂丂俶 偑柍柕弬偱偁傞側傜偽丄 俠倧値倱倝倱 偼俶偱徹柧壜擻偱偼側偄
丂丂偙偙偱丄
丂丂丂丂丂丂丂丂丂丂

丂丂仸丂丂戞俀晄姰慡惈掕棟偐傜丄偦偺媡傕傑偨惉棫偡傞丅偡側傢偪丄岞棟宯偵柕弬偑娷傑傟傞側傜偽丄侾乯 偦偺岞棟宯偐傜偳傫側柦戣偱傕徹柧偱偒丄偝傜偵丄俀乯 岞棟宯帺懱傕柍柕弬偱偁傞偲偄偆庡挘傕徹柧偱偒傞丄偲偄偆旂擏側偙偲偑抦傜傟偰偄傞両丂乮丂仺丂俇丏乮侾乯丄 俈丏乮俀乯 乯
丂丂丂丂丂戞侾掕棟丄戞俀掕棟偺懳嬼傪偲傞偲丄
丂丂丂丂丂丂丂丂丂丂丂侾丏丂俙丂仺丂乣俛丂丗柍柕弬側傜偽晄姰慡丂丂佁丂丂俛丂仺丂乣俙丂丗傕偟寢壥偑姰慡偱偁傞側傜偽丄岞棟宯偼柕弬偟偰偄傞
丂丂丂丂丂丂丂丂丂丂丂俀丏丂俙丂仺丂乣俠丂丗柍柕弬側傜偽丄偦偺柍柕弬惈傪徹柧偱偒側偄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂佁丂丂俠丂仺丂乣俙丂丗柍柕弬偱偁傞偙偲傪徹柧偱偒偨側傜偽丄岞棟宯偼柕弬傪娷傓
丂丂丂丂丂丒丒丒丂姰慡乮徹柧偱偒側偄偙偲偑柍偄乯偐偮柍柕弬側寢壥傪傕偨傜偡恄偼丄偦偺撪晹偑榑棟揑偵柕弬偟偰偄偰摉慠乮嶰埵堦懱丄侾亄侾亄侾亖侾乯