丂丂丂丂丂丂丂丂俆丏丂揹巕夞楬偺憡屳尵媦
丂丂巚嶕偵偍偄偰丄侾乯 榑棟揑恀婾傕丄俀乯 乮俀恑朄偲偟偰偺乯偡傋偰偺悢抣傕丄乭侽乭丄乭侾乭偺傒偱昞尰偝傟傞丅乮悢抣偺応崌偼寘忋偘偱昞帵偝傟傞丅乯 偦傟偩偗偱側偔丄帺慠偵偍偄偰傕丄揹婥偺僨僕僞儖怣崋傕揹埵嵎偺乭俴乭丄乭俫乭乮亖 偦傟偧傟乭侽乭丄乭侾乭乯偲偄偆俀庬椶偺抣偱昞尰偱偒傞偺偱丄偙偺僨僕僞儖怣崋傪巊偭偰懡偔偺寁嶼傪偡傞偙偲偑偱偒傞丅
丂丂乮侾乯丂僎乕僨儖柦戣偺暔棟壔丗
丂丂偝偰丄榑棟揑側乭寛掕晄擻柦戣乭偵憡摉偡傞傕偺偼丄揹巕夞楬偵傕尰傟傞丅揹巕夞楬偼暔棟揑側儊僇僯僘儉偱偁傞偐傜丄偙偺寛掕晄擻柦戣偺傗傝偲傝偼帪娫揑偵憒堷乮偦偆偄傫乯偝傟偰丄偁傞廃攇悢傪傕偮揹婥揑側乭敪怳乭尰徾偲側傞丅
丂丂壗傜偐偺曽朄偱 弌椡偺堦晹傪 埵憡傪斀揮偟偰傕偆堦曽偺擖椡偵僼傿乕僪僶僢僋偡傞婡峔傪嶌傞偲丄憹暆婍乮傾儞僾丄擻摦慺巕乯偼丄懠偺庴摦慺巕乮僐儞僨儞僒乕 俠丄掞峈 俼丄僀儞僟僋僞儞僗 俴乯偺慻崌偣偵傛傞帪娫揑抶傟傪敽偭偰丄弌椡怣崋偺斀揮傪孞傝曉偡丅
丂丂乮們倖丏丂侾偮偺傾儞僾偱怣崋傪斀揮偡傞乭晧婣娨乭偼丄傾儞僾偺弌椡傪彮偟壓偘傞偩偗偱偁傞丅晧婣娨偼丄夞楬偺婑惗敪怳傪杊偓 憹暆摦嶌傪埨掕偝偣傞偨傔偵梡偄傜傟傞丅乯
丂丂俀偮偺傾儞僾偵晧婣娨傪偐偗傞儊僇僯僘儉偼丄榑棟揑偵斲掕揑側乭帺屓尵媦乭傗乭憡屳尵媦乭傪慻傒崬傓偙偲偵憡摉偡傞偐傜丄敪怳夞楬偼 暔棟揑側乭僎乕僨儖柦戣乭偱偁傞偲尵偊傞丅
丂丂傕偪傠傫丄敪怳偼弮悎側暔棟尰徾偱偁偭偰丄暔帠偺恀婾傗柕弬傗慞埆偺堄枴傪帩偨側偄丅僐儞僺儏乕僞乕偵傛傞寁嶼寢壥偵偮偄偰傕丄恖娫偑偦偺堄枴晅偗傪峴偆丅
丂丂乮俀乯丂柍埨掕儅儖僠僶僀僽儗乕僞乕丗
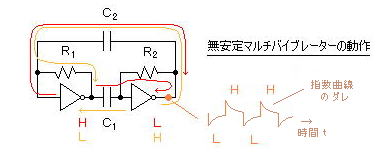
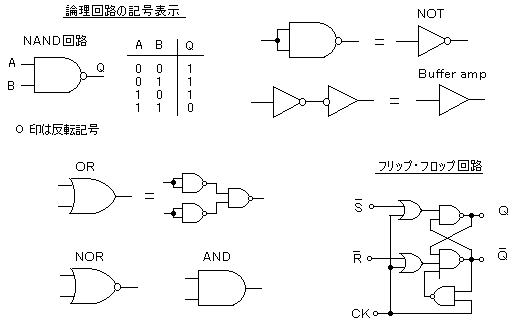
丂丂揹尮傪擖傟傞偲帺摦揑偵敪怳偟偰僷儖僗攇宍傪嶌傝弌偡夞楬偱丄僨僕僞儖夞楬偺敪怳婍偲偟偰傛偔梡偄傜傟傞丅偙傟偼丄揹巕夞楬偵偍偗傞乭憡屳尵媦乭偺宍偱偁傞丅乮仏丂僨僕僞儖夞楬偺婎杮梫慺偼丄俶俙俶俢丄俶俷俿 偱丄乭斀揮乭婡擻傪帩偮丅乯
丂丂丂丂丂丂丂丂丂丂丂丂丂
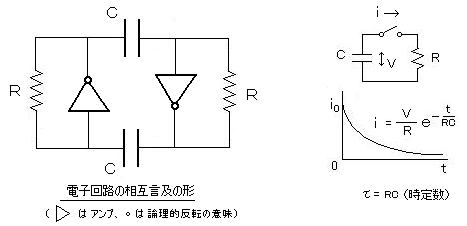
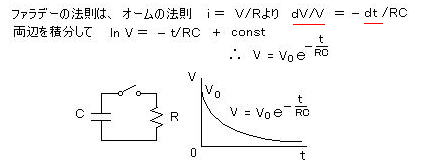
丂丂偨偲偊偽丄敿摫懱傾儞僾偺斀揮偺擖椡摦嶌揹埑乮乭俫乭丄乭俴乭 忬懺傪擣幆偡傞 僗儗僔儂乕儖僪儗儀儖乯傪丄偦傟偧傟 倁俴 亖 侾丏係倁
 丄倁俫 亖係丏俆倁丄丂俠 亖 係丏俈兪俥丄俼 亖俁俁倠兌 偲偡傟偽丄
丄倁俫 亖係丏俆倁丄丂俠 亖 係丏俈兪俥丄俼 亖俁俁倠兌 偲偡傟偽丄丂敿廃婜丂俿 亖 亅俠 俼 倢値 乮倁俴/倁俫乯丂亖 侽丏侾俉乮倱乯
丂丂丂丂丂丂亪丂丂倖丂亖 侾/乮俀俿乯 亖 俀丏俉乮俫倸乯
丂乮傾儞僾偵偼丄俿俿俴 俬俠 偺俈係俴俽侽侽丒丒丒俶俙俶俢夞楬亊係儢丄俈係俴俽侽係丒丒丒俶俷俿夞楬亊俇儢 側偳偑巊偊傞丅 俠1丒俼1偲俠2丒俼2偺抣傪曄偊傟偽丄暆偺堎側傞曽宍攇偵側傞丅乯
丂丂扨埨掕丄偍傛傃丄憃埨掕儅儖僠僶僀僽儗乕僞乕傕丄榑棟揑側乭晄掕乭忬懺傪嶌傞丅憃埨掕儅儖僠僶僀僽儗乕僞乕偺摦嶌偼丄僼儕僢僾丒僼儘僢僾夞楬乮僼儕僢僾丒僼儘僢僾 亖 僔乕僜乕丄偓偭偙傫偽偭偨傫乯偺摦嶌偲摨偠偱偁傞丅
丂丂丂丂丂丂丂
丂丂仏丂丂傑偨丄帺屓尵媦偵憡摉偡傞夞楬偼丄帺椼敪怳夞楬側偳偑嫇偘傜傟傞丅偙傟偼 俴俠 嫟怳婍偐傜弌椡傪丄捈慄惈偺椙偄傾僫儘僌憹暆婍乮僩儔儞僕僗僞乕乯偵僼傿乕僪僶僢僋偡傞夞楬側偺偱丄弌偰偔傞攇宍偼惓尫攇偱偁傞丅俴俠嫟怳婍偺廃攇悢偼丄 倖 亖 侾/乮俀兾併乮俴俠乯乯丅
丂丂丂丂丂丂
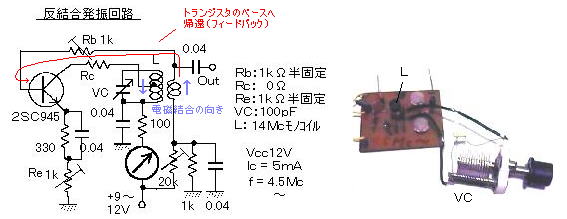
丂丂仏仏丂俴俠 嫟怳婍偺戙傢傝偵悈徎怳摦巕傪梡偄傞偙偲傕偱偒傞丅偙偺応崌丄悈徎偺埑揹摿惈偵傛傝婡夿揑嫟怳偲側傝丄傗偼傝僩儔儞僕僗僞乕偺儀乕僗傊惓婣娨偡傞丅乮悈徎偺斅岤曽岦偺挻壒攇偺懍搙暘抶傟偰婣娨丅敪怳廃攇悢偺惛搙偼悈徎偺婡夿揑惛搙偵傛傞丅乯
丂丂偦偺懠丄暘晍掕悢夞楬丄儅僌僱僩儘儞側偳丄壗傜偐偺宍偱僞僀儈儞僌傪抶傜偣偨惓婣娨傪偐偗傞宍偱敪怳婍偲側傞丅
丂丂乮俁乯丂巜悢娭悢偵傛傞帺慠偺婰弎丗
丂丂曽掱幃偲偼丄曄悢 倶 偵偮偄偰偺乭帺屓尵媦乭偺宍乮楢棫曽掱幃偺傛偆側暋嶨側傕偺偵偼乭憡屳尵媦乭傕宍惉偱偒傞乯偱偁傝丄偦偺柍尷偺壜擻惈偺拞偐傜丄偦傟傪乭枮偨偡乭夝丄偁傞偄偼丄娭悢傪媮傔傞惈幙偺傕偺偱偁傞丅
丂丂帺慠偺拞偵偁傞僒僀僋儕僢僋側暅尦偺宍懺傪尒偰傒傛偆丅師偺丄旝暘曽掱幃偲偦偺夝傪峫偊傞丅
丂丂丂丂丂丂丂
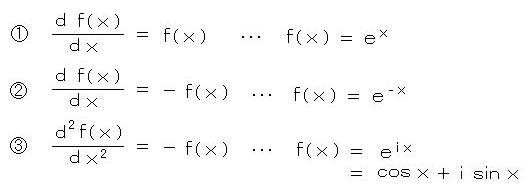
丂丂丂嘆 偼丄 倖 乫亖 倖乭 亖 丒丒丒 亖 倖丂偱偁傝丄 倕倶倫 倶丂偺掕媊偦偺傕偺偱偁傞丅 偟偐偟丄 倕倶倫 倶丂宆 偺娭悢偼 帺慠奅偵偼懚嵼偟側偄丅
丂丂丂嘇 偼丄侾夞旝暘偡傞偲 亅晞崋偑晅偔暔棟朄懃丗丂
丂丂丂丂丂丂僼傽儔僨乕偺朄懃丂丒丒丒丂
丂丂丂偙傟偼 僆乕儉偺朄懃丂倁 亖 倝 俼丂傪梡偄偰丄曄悢暘棧宍偺旝暘曽掱幃偵偡傞偙偲偑偱偒丄娙扨偵夝偐傟傞丅
丂丂丂丂丂丂丂丂丂丂丂
丂丂丂偡側傢偪丄倕倶倫乮亅倶乯 宆偺娭悢偲側傝丄帺慠偵偩傜傝偲偟偨乽巰乿偺暔棟尰徾傪昞傢偡丅擬椡妛偺婰弎傕丄偙偺 曄悢暘棧宆偺侾奒偺旝暘曽掱幃偲 倕倶倫乮亅倶乯 偺宍偲側傞丅偽傜偽傜偺嵒棻偺傛偆側尨巕丄暘巕偼丄摑寁椡妛偵傛偭偰偙偺乭巰偺 倕 乭偑尰傟偰偔傞丅乮僗僞乕儕儞僌偺岞幃 仺 儃儖僣儅儞偺幃 丗 俽 亖 倠 倢値 倂乯
丂丂丂嘊 偼丄丂倖 亖 倕倶倫乮倝 倶乯 偲偟偰丄 倖乫 亖 倝 倕倶倫乮倝 倶乯丄丂倖乭 亖 亅倕倶倫乮倝 倶乯 亖 亅倖丂偺傛偆偵丄俀夞旝暘偟偰亅晞崋偵側傞暔棟朄懃偱偁傞丅僼傽儔僨乕偺朄懃偺倁偵 僿儞儕乕偺朄懃偺倁傪戙擖偡傞偲乮俴俠嫟怳夞楬丄揹棳偺曽岦偑媡偵側傝丄晞崋偑媡偵側傞偙偲偵拲堄乯丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
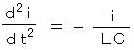 丂丂丄丂丂丂丂丂丂丂丂丂偙偺夝偲偟偰丄
丂丂丄丂丂丂丂丂丂丂丂丂偙偺夝偲偟偰丄丂丂丂丂丂丂丂丂丂
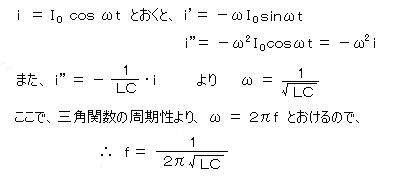 丂丂偲側傞丅
丂丂偲側傞丅丂丂丂偙傟偼丄倁傗俻乮揹壸乯偵偮偄偰傕惉傝棫偪丄俴俠嫟怳夞楬偺塱懕揑側揹婥揑怳摦尰徾傪昞尰偟偰偄傞丅乮揹婥掞峈偑柍偗傟偽塱懕揑偵怳摦偡傞丅乯
丂丂丂偙偺傛偆側丄俀奒旝暘曽掱幃偺夝偱偁傞丄巜悢娭悢偺檖偵嫊悢扨埵偑擖偭偨 倕倶倫乮倝 倶乯 宆偺娭悢偼丄乽偄偺偪乿偺暔棟尰徾傪昞傢偟偰偄傞丅 倕倶倫乮倝 倶乯 偺宍偼 検巕椡妛偺攇摦娭悢偵尰傟偰偄傞偺偱丄儈僋儘偺悈柺壓偺忬懺偼丄偙偲偛偲偔丄憂憿庡偺乭偄偺偪乭偱枮偪堨傟偰偄傞偙偲偵側傞丅
丂丂丂偟偨偑偭偰丄晧婣娨乮亖榑棟揑偵斀揮偡傞帺屓尵媦丄憡屳尵媦乯偵傛傞敪怳夞楬偺揹婥怳摦偼丄憂憿庡偺偄偺偪傪徾挜偟偰偄傞偲傕尵偊傞丅