1. 数学の3定数(1):
われわれが通常 理性的に認識する計量感覚は2方向である。
「論理」的には、真:偽、+:-、正:負、(デジタル信号の)1:0、善:悪、白:黒、表:裏、右:左、存在する:存在しない、 ・・・・・ などの、方向だけがあって量の無い”対”の概念が存在する。論理学や数学の証明法として、”背理法”は、この二者択一の”論理性”に基づいている。(*)
一方、「数学」的には、論理的な2方向に、さらに、”かさ”の概念が付け加えられ、大:小、長い:短い、高い:低い、広い:狭い、重い:軽い、遠い:近い、濃い:薄い ・・・・・ などがどの程度になるかという”量的概念”が存在し、それらが抽象化され、① 基数、および、② 順序数(あるいは”序数”)が形作られた。 それらの量を数学的な値に対応させ、図形や計算などの理論を形成することができる。たとえば自然数論の公理系に和と積の定義を入れておけば、帰納法の公理によりすべての自然数について四則演算(和差積商+冪)の体系が出来上がる。
(ただし、”3すくみ”の論理・・・じゃんけんのグー・チョキ・パー、色彩認識、音色認識・・・ のような特殊な理性的感覚もある。現代数学ではさらに抽象化され、一般的な量感覚を問題にしない分野も多い。)
”証明”は、論理学や数学にとって切っても切れない関係にある。証明されていない数学的命題は、数学的真理(定理)ではなく、あくまで”予想”にすぎない。コンピューターで計算して非常に確からしいけれども、結局 間違っている、という実例はいくらでもある。(たとえば、(-1)の√(-163)乗 を数値計算した結果の 262537412640768743.99999999999925007・・・・ はもう少しで整数であった!)
これが物理学の証明や天文学(の証明?)などとの決定的な違いである。
(1) 3つの数学定数:
一般に、数学定数と言われるものは、正真正銘のもので、古代ギリシャから現在に至るまで たったの 3つ ・・・ 円周率 π、虚数単位 i 、自然対数の底 e 、しか知られていない。他は、派生的、あるいは、単に伝統的な定数である。
これらの数学定数は、3つの数学的思索の発祥地点と密接な関係があり、それぞれ 初等的な3つの数学分野の代表的な数になっている。すなわち、
1) 初等幾何学: 円周率 π、 2) 初等代数学: 虚数単位 i 、 3) 解析学: 自然対数の底 e
であり、それらの本来全く異なる分野の3定数が 「オイラーの恒等式」という 1つの単純な形に合体する、という 数学史上最も驚くべき、美しい関係が存在する。この関係は、純粋に理論的に導かれたもので、我々はそれを直感的に認識することはできない。
・・・・ 神の「三位一体」と同じ。 父・子・聖霊の三位一体は聖書の多くの文脈から来るものであるが、それが理性でわかったとする議論はすべて間違い。
オイラーの恒等式の左辺の π は御父、 e は御子、 i は聖霊、右辺の -1 は神の愛 を象徴していると考えられる。
ここで、右辺の-1 は”論理性”を表現している。( → 3.、4.)

1) 幾何学の π:
パブロフの犬という、古典的条件付けの実験によると、真円と明らかな楕円をイヌに見せてからそれぞれ別の命令を出し、条件付けが充分行われてから、その見せる円と楕円の形状を次第に接近させていく。すると、あるところで、イヌは識別できなくなり狂ったような状態になったそうである。この犬の”知性”の限界はこの辺だったらしい。
また、サルの視覚野の細胞に電極を刺してその興奮状態を調べる最近の実験では、ある特定の細胞だけが サルが見た特定の形状(+、-、l、○、×、△)に反応するそうである。このように、寸法を度外視した”簡単な形状”については、動物でも感覚的に識別できるようである。サーカスの犬が数字を識別するのは、数としてではなく形状として認識しているからである。
我々にとっても、漢字や数字を交えた文章が、ひらがな あるいは ローマ字だけの文章よりもはるかに読みやすいのは、文字や熟語を視覚的に認識しているからである。
円周率 πは、2次元以上の広がり(平面、空間、超空間)があって初めて考えられる定数であり、”求心的”、あるいは、”周期的(サイクリック)”な思索、思想と関係が深い。おそらく、いろいろな神様を崇拝していた昔の素朴な人々は、円周率を聖なるものと見ていたことだろう。 円周率は、直径とその両端を通る円の周の長さとの比: 円周の長さ 2πr であるが、円の面積 πr2 や 球の体積 4/3 πr3 、円錐の体積 1/3 πr2h などとして古くから知られていた。 しかし、π の値を具体的に求める方法は、オイラーの関係式を変形して無限級数から計算する一連の方法が発見されるまで、実に1500年もの間、唯一、アルキメデス法(アルキメデス、BC287?-212)しかなかった。
それは、単位円(=半径1の円)に外接および内接する正多角形の辺の長さを求めていく方法であり、視覚的には考えやすい方法であるが、実際の計算は困難だったと予想される。
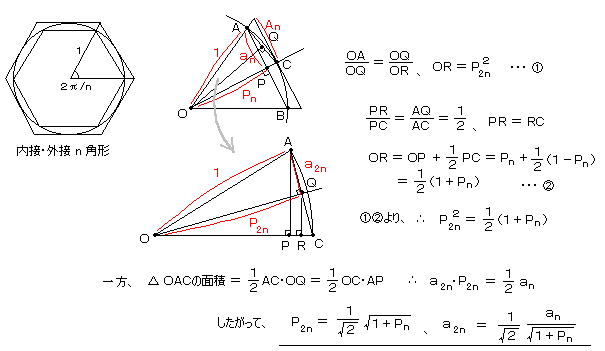
内接正n角形の内周は 2nan、 外接n角形の外周は 2nAn、 円周は 2π だから、
nan < π < nAn 、 na2n < π < nA2n 、 ・・・・・ のように漸近する。
たとえば、 n=3 のとき nan = 3√3 /2 、 nAn = 3√3
n=4 のとき nan = 2√2 、 nAn = 4
正方形から出発して、上記の角度の2等分を繰り返すと、
n=16 のとき 3.1214・・・、 3.1826・・・
n=64 のとき 3.14033・・・、 3.14411・・・
n=2048のとき 3.141591422・・・、 3.141595118・・・
アルキメデスは、n=3 から始めて、正96角形の場合を、平方根を分数に近似して計算し、
3+10/71 < π < 3+1/7 、すなわち、 3.1408 < π < 3.1428 を得た。
・ ピタゴラスの定理の証明は、かなり図形のパターン認識のアイディアによっている。また、具体的な数の代わりに任意の長さを文字で表現している所がこの定理の汎用性が高い理由である。

問題を、図形パズルやグラフなどに視覚化すると分かりやすくなる場合が多い。(これは、人間の後頭葉の認識野と視覚野が近いので回路がつながりやすいためと考えられる。 つまり、”明らかに、見るからに、・・・?”)
時代は飛ぶが、
・ ガウスは小学生の頃、1 から 100 までの数の和を暗算で瞬間的に計算した。
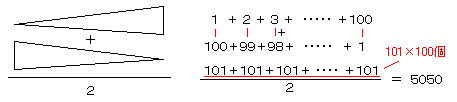
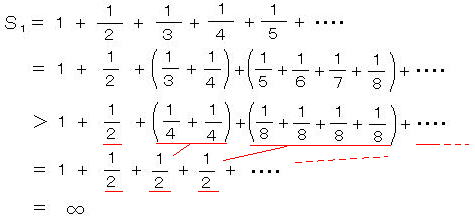
・ 調和級数の発散(ニコル・オレスム、1350)
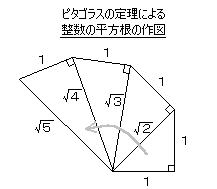
・ ギリシャ時代は、定規とコンパスだけによって、平方根の長さの作図をも行っていた。作図可能であることと、有理数であることとは深い関係がある。
定規とコンパスのみを有限回使用して作図ができるのは、任意の有理数(=整数の分数)と、有理数の平方根までであって、次の式の数(a、p、q、r はすべて有理数)までが作図可能であることが知られている。
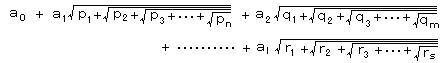
・ 正 n 角形の作図について、ガウス(1777-1855)は、このユークリッド的方法で作図可能であるのは、
のときに限られることを証明した。このような素数 pi は、 k = 0、1、2、3、4 に対し、3、5、17、257、65537 の5つだけ知られている。 単位円に内接する 正17角形の1辺の長さは、
* 古くからある証明法として、”背理法”がある。背理法(=帰謬法(きびゅうほう))は、白か黒か2つに一つである”論理性”から証明する方法 ・・・ ある命題が 偽 であることを証明するために その命題が 真 であると仮定して矛盾を導く ・・・ であり、演繹法、帰納法などと共に数学の証明法として非常によく用いられる。(ソロモンの知恵(Ⅰ列3:16-)に近い) 一例として、ユークリッド(BC365?-275?)による「素数の無限性」の証明をしてみよう。
素数とは、その数と1以外に割り切れない(約数が無い)数である。
仮に、最後の素数が Pn だったとすると、A を Pn までの素数をすべて掛け合わせ 1を足した数とする。
A = 2・3・5・ ・・・ ・Pn + 1
Pn は最後の素数なので、A は合成数であるから、Pn 以下の素数で割り切れるはずである。
A/2 = (3・5・7・11・ ・・・ ・Pn) 余り 1
A/3 = (2・5・7・11・ ・・・ ・Pn) 余り 1
A/5 = (2・3・7・11・ ・・・ ・Pn) 余り 1
・・・・・・・・
A/Pn = (2・3・5・7・ ・・・ ・Pn-1) 余り 1
すなわち、A はどのような素数によっても割り切れない。ゆえに、A 自身は素数である。しかし これは、Pn より大きい素数が存在しないという仮定に反する。したがって、素数は無限に存在する。