＊　　中性子干渉計の実験：


　　中性子干渉計の一連の実験は、物質が波動であると同時に粒子であることを強く印象付けるものである。物理量の期待値は古典力学の運動方程式に従う。（エーレンフェストの定理）
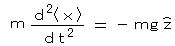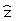　　　　　　　　　　　　　ただし　　　は ｚ 方向の単位ベクトル。
　　だから、原子炉から水平方向に飛び出た中性子線は、一様な重力 ｇ によって自由落下し放物線軌道を描いて −ｚ 方向に加速する。このとき 中性子の速さが増し波長が短くなるので、分割された２本の中性子線の軌道に高さの差があると 位置エネルギーの差が現れ、再合成されたとき その波長差�刄ﾉによる干渉が現れる。
　　　　

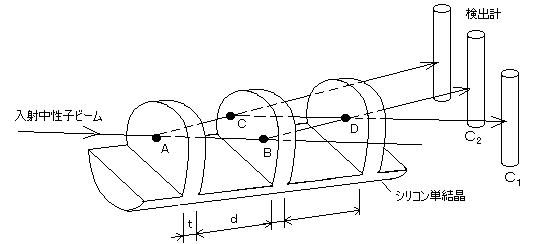
　　原子炉からの 波長λ＝1．445Åの中性子（ｖ ＝ 2800ｍ/ｓ、波束の長さ ＝ 約５ｍｍ）を、直径５ｃｍ、長さ８ｃｍの格子欠陥の無いシリコン単結晶に ｔ ＝ 0．4354±0．00008ｃｍ、ｄ ＝ 2．72936±0．00009ｃｍの三枚の耳を切り出した中性子干渉計に、ブラッグ角で入射させる。 １個の中性子は、Ａで透過波とラウエ散乱による波に分かれ、Ｂ、Ｃでもう一度繰り返して、Ａで分割された１個の中性子は Ｄで再び合流し それ自身で干渉して、検出計に入る。（中性子は１００個/ｓくらいの割合で入射するが、通過時間 ＝ ３×１０‐5ｓで波束の長さ ＝ 約５ｍｍなので、２個の異なる中性子が互いに干渉する確率は１０‐9 程度で無視してよい。）

　　ここで、ＡＢ軸で単結晶を回転させ ＣＤをＡＢより高くすると、ＣＤ（約４ｃｍ）を通ったとき位置エネルギーだけ運動エネルギーが小さくなり ｐ ＝ ｈ/λ に従って波長が長くなる。この速さの違いは 高さの差 １ｃｍに対し �凾�/ｖ ＝ １０‐8 程度なので、異なる経路を通ってきたコヒーレントな波は干渉して、回転角の変化（０〜３０度の範囲）に対して、検出計 Ｃ1 の中性子のカウント数が±５〜２０％増減して、強め合ったり弱め合ったりの振動する曲線が得られる。中性子干渉計は １０9個の波のうち１０波長くらいのずれを検出できる。（1975）

　　　＊＊　　超流動と超伝導：


　　�@）　　同種のボソン（ボース粒子）Ｎ個が同一の波動関数で表される状態にあるとすると、 Ｎψ*ψ は粒子数密度の期待値（マクロな粒子密度）を与え、　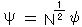　、　　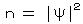　と書ける。（Ψ：　マクロ波動関数）
　　ボース粒子（質量ｍ）の流れは、　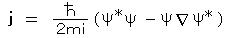　　　　となり、確率の流れではなく、マクロな粒子流密度を意味する。　Ψを、　　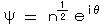　のように 絶対値と位相とに分けると、
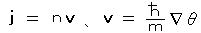　　　　　　　　　　　　　　　　　　　　　　　　　（ ｖ はマクロな流速）　となる。
　　この ｖ は、スカラー量θの勾配∇θ に比例するから、
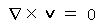　　　　　　　　　　　　　　　すなわち、局所的な回転が禁じられた流れであり、粘性を示さない。（超流動体）
　　ただし、渦糸が存在して、量子化された角運動量をもつことができる。この場合、θ は 渦糸のまわりを一周するごとに ２π の整数倍だけ値が変化する無限多価関数であり、 マクロ波動関数 Ψ は 角運動量が 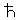の整数倍しかとらない状態に量子化される。 ｖ をマクロな半径の円周に沿って積分すると、
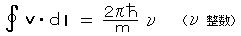　　　　　　　　　　　　　　のようになり、左辺は古典流体力学で ”渦度”（あるいは ”循環”）とよばれるマクロな量になる。（渦の量子化）
　　超流動体の乱流の扱いは、古典流体よりも扱いやすい。


　　�A）　　超伝導の場合も同様に、荷電物質がコヒーレント状態にあると考え、超流動の”回転”に対して ”磁場”が対応する。その際 注意すべきは、磁束密度 Ｂ ではなく、　Ｂ ＝ ∇×Ａ　で定義される ベクトルポテンシャル Ａ の導入が必要となる。（ゲージ理論 および アハラノフ・ボーム効果から、ベクトルポテンシャルの方が本質的である。 任意のスカラー ｆ に対し、Ａ → Ａ + ∇ｆ としても物理的状況は変わらない。）
　　マクロ波動関数が 超流動体と同じ　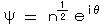　で表されるならば、
　　　　　　　　　　　　　　　　　　　　　　　　　　θ　→　θ−（ｅ’/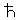）ｆ　　（ｅ’ は 凝縮粒子の電荷）
　　の置き換えを行う。
　　また、マクロな流速 ｖ と それに伴う 電流密度 ｊ ＝ ｎｅ’ｖ　は、ゲージ変換に対して不変であるはずなので、
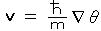　　　の ∇θ を、　　　　　∇θ　→　∇θ−（ｅ’/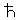）Ａ　　　　で置き換える。
　　したがって、　電流密度は、　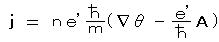　　　　　　となる。
　　ここで、凝縮粒子密度 ｎ を定数とみなして良い場合には、
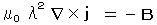　　　　　　　　　　　　、　ただし　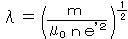　　　（λ　磁気侵入長）　
　　となり、
　　磁気が侵入する厚さ λ の表層部で外部磁場を打ち消す電流磁場が発生し、表層部以外ではすべて　Ｂ ＝ 0　である。（マイスナー効果）
　　磁束も量子化され、　　　　　　　、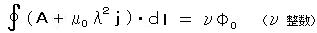　
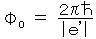
　　となり、 Φ0 は 磁束の次元をもつ定数である。
　　超伝導体中の電子は、ほとんどの場合、電子が２個づつペア（クーパー・ペア）になっていて凝縮をおこし、内部自由度をもたない状態になっていることが知られている。

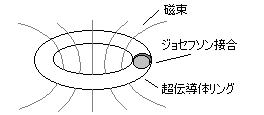
　　超伝導はジョセフソン素子に応用されている。このジョセフソン接合を含むリングがつくる マクロの磁束を観測することによって、マクロなトンネル電流やバイアス電圧の ”零点振動”に基づく”量子力学的ゆらぎ（零点エネルギーの期待値： 〈Ｅ〉0 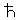＝ ω/２）”が、量子化された磁束の振動（振動数 ＝ （ ｌ ａ 〉、ｌ ｂ 〉 状態のエネルギー差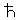）/）を測定することによって、磁束に関するマクロの不定状態として観測されるはずである。これは、”シュレディンガーの猫”である マクロのコヒーレンス状態（ＭＱＣ）である。（ただし、零点振動は散逸過程での損失が大きく 現在のところ測定は成功していない。常圧で液体ヘリウムが固化しないのは零点振動による。））

　　　　　　　　　　　　　　本文５．へ戻る　　　　　　本文１．へ戻る