�@�@�@�@�@�@�@�@�@�P�D�@���f�����ɂ��莮���i�P�j�@�E�E�E�@���f����ʂ̓���
�@�@���R�̑��̓����́A�����́h���f���̔g���h�ł���A�K�R�I�ɁA�h�w�����h�̌`���ŕ\�킳��邱�Ƃł������B
�@�@������ ����ɁA�g�����i�m���U���j ����� ���ۂɌ���������̂��낢��ȑ���l �����߂ɁA���f���̗̈�ɂ������{�T�O�m�ɂ��Ă����Ȃ���Ȃ�Ȃ��B���Ȃ킿�A��ԃx�N�g������p�f�Ƃ����� ��Ԃƕ����ʂ�\�����邽�߂̐��w�I�ȗʂ��߂�K�v������B�i�ł��邾���L���K�p���邽�߂� �����̈�ʓI�Ȓ莮�����s�Ȃ��ƁA���Θ_�I�ʎq�͊w�ł��A��̗ʎq�_�ł����l�ɗ��_�\�������邱�Ƃ��ł���B�j
�@�@�����̒莮���ɂ����Č�����A���R�̑��̓����ƂȂ���̂́A���̐��w�I�Ȑݒ肪�A��Ɂh���f�����Ƃ̑��h�̌`���ɂȂ��Ă��邱�Ƃł���B���Ƃ��� �f���q������ �t��o�A�Ώ̐��Ȃǂ̐����̗��_�́A���̕��f�����̐ݒ肪�����ł���A�܂��A�����ɔ��ɂ悭�����Ă���B
�@�@�����̓����� �����l�ɕϊ����鎞�Ɍ����A���̐������ł͂Ȃ��A�ނ��� �n����ł����_�̘_�����i�Q�������A�{ �ɑ��� �| �̗v�f�j������������B
�@�@�i�P�j�@��Ԃ̒莮���F
�@�@�g�Ƃ��h���\�h�Ƃ������Ƃł���A��ԂƏ�ԂƂ��d�ˍ��킹�����̂� �Ώۂ̂Ƃ肤���Ԃ̈�ł���Ƃ��������������Ă���B�i�d�ˍ��킹�̌����j
�@�@�i�i���j �d�ˍ��킹�����藧�̂� �n�� �ʑ��̑������i�R�q�[�����g�ȁj�h��������h�̏ꍇ�Ɍ���B �ʑ������ꂽ�h��������h�ł� ���͋N����Ȃ��B�@�i�� ��q�j�j
�@�@�Ώۂ̂Ƃ肤���Ԃ��A�f�B���b�N�̋L�� ���@�r �i��ԃx�N�g���A�P�b�g�x�N�g���A�P�b�g�Ɠǂ��j�ŕ\�킷�ƁA���Ƃ��A�d�q���̋��x �� �i�X�J���[�j��ς��Ă����̏�� �� �i�x�N�g���j�͕ς��Ȃ����Ƃ�\������̂ɁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�d�ˍ��킹�̏�Ԃ́A�@�@
�@�@���̂悤�ɁA��Ԃ̓x�N�g���ł����āA���̐��������B ���̂悤�ȋ�Ԃ́A�x�N�g����ԁi���`��ԁj�ƌĂ��B
�@�@�@�@�@�@�@
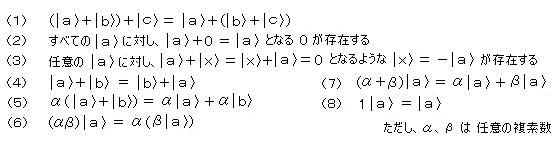
�@�@���Ƃ��A�R�q�[�����g�ȓd�q����[�U�[���Ȃǂ� ������Ԃ̏d�ˍ��킹�́A
�@�@�@�@�@�@
�@�@�����ŁA���̃P�b�g�x�N�g���ɑ��A �h�����ȃx�N�g���h �q �� �� �i�u���x�N�g���G �P�b�g�x�N�g���ƍ��킹�� �u���P�b�g�i���ʁj�̈Ӗ��j������ƁA �P�b�g�x�N�g���ƃu���x�N�g���Ƃ̐ρi�����j
�@�@�u���x�N�g�����P�b�g�x�N�g���Ɠ��l�� ���ׂĂ̒l���Ƃ蓾��̂ŁA��̑Ώیn�̏�Ԃ� �u���x�N�g���̑g �o�q �� ���A�q �� ���A�E�E�E�p �ł��A�P�b�g�x�N�g���̑g �o�� �� �r�A�� �� �r�A�E�E�E�p �ł��ǂ���ł��\�킹��B�@���҂̊W�́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
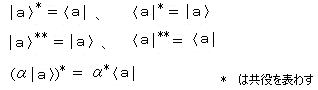
�@�@���ςɂ��ẮA�@
�@�@�܂��A�������Ƃ́A���q�� �ʒu�A�^���ʁA�p�^���ʁA�G�l���M�[�A�d�ׂȂǂ� ����ɂ���Ēl��m�邱�Ƃ̂ł��� �n�◱�q�̑����ł���B��Ԃ��ǂ̂悤�Ɏw�肳��邩�́A���̌n�̕����ʂ��ǂ̂悤������l�������ɂ��B���̂悤�ɁA��Ԃƕ����ʂƂ݂͌��ɋK�肵�����W�ɂ����B
�@�@�i�Q�j�@�͊w�ϐ��̒莮���F
�@�@�����͊w�n�i���q�̌� ���@�A�͊w�ϐ��̐��i���R�x�j �m �� �R�� �� ���j�j��ݒ肷��ꍇ�A�ł���ʓI�ɒm���Ă��闝�_�́A���O�����W���`���ƃn�~���g���`���ł���B����͗��j�I�ɂ͌ÓT�͊w�̐����Ƃ��Č��ꂽ��͗͊w�ł��邪�A���e�I�ɂ͗͊w���͂邩�Ɉ�ʓI�ȗ��_�ŁA�}�N�X�E�F���̓d���C�w�⑊�ΐ����_�� ���̌`���ŕ\�킷���Ƃ��ł���B
�@�@�@�@�R�����̎��R�x�Ƃ��� ���q���ʒu
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@���� ��0 �� ��1 �i��1 �� ��0�j�̊Ԃ̌n�̕ω��ɂ��āA
�@�@�@�@�@�@
�@ �C�ӂ̕ϕ��@�����i �� �j�@���@�����i �� �j �{ �������i �� �j�@���s�Ȃ��ƁA�@
�@�@�@�@�@�@
�@�@�E�ӑ�P���� 0 ���A
�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�킴�킴 �^�����������A��ʉ����ꂽ�ʒu���W�Ǝ��Ԕ����Ƃ̊��ł��郉�O�����W���`���ɍē��o���闝�R�́A���̌`���ŏؖ�����Ă��鎖��n�����Ώ̐��Ȃǂ̐����������o�����߂ł���B
�@�@�܂��A�^���ʂ�ϐ��Ƃ��� �n�~���g���`���ɂ��āA
�@�@�@�@�@�@�@�@�@�@
�@�@���x
�@�@�@
�@�@���`����B �n�~���g�j�A���́A�S�G�l���M�[�ɑ������镨���� �𐳏����W�Ɛ����^���ʂŕ\�킵�����̂ł���B �l����n���A�ǂ̂悤�ȗ͊w�I���R�x�������A�ǂ̂悤�ȑ��ݍ�p�����邩�́A���ׂ� ���O�����W�A����n�~���g�j�A���̒��Ɏ������B
�@�@�i�R�j�@�����W�F
�@�@�g�����ɑ��� �^���ʂ��A
�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�V�����f�B���K�[�������i�P�|�Q�j�́A
�@�@�@�@
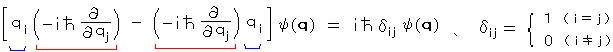
�@�@�ƂȂ�B �Ձi���j ����p���鏇�����Ⴄ�� ���̍��� �v�����N�萔 �� �ɔ�Ⴗ���B
�@�@�V�����f�B���K�[�������������@�I�ɓ����ꂽ�̂ɔ�ׁA���̎��́A�����ƈ�ʉ����ꂽ�Ӗ������ƍl������̂ŁA���̂悤�� �ʎq���̋K�� ���Ȃ킿�A��p�f���h�����W�h �����肷��B
�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i
�@�@�����ʂ͂��ׂĐ������W�Ɛ����^���ʂƂ̊��ł���B���������āA���ׂĂ������ʂ� ��p�f�ƂȂ�A�C�ӂ̂Q�̕����ʂ̊Ԃ̊W�i���@�s�m�萫�W �Ȃ� �j�́A���̌����W���瓱�����Ƃ��ł����B
�@�@�E�ӂ� �����P�� �� �� ��|�P �������Ă��邱�Ƃ́A�i�P�j�� �h��ԁh�����f���ŕ\�킳�ꂽ�悤�ɁA�h�����ʁh�ɂ��Ă����f�����{���ł��邱�Ƃ������Ă���B
�@�@�i�S�j�@������p�f�F
�@�@�ȏ����x�܂Ƃ߂�ƁA
�@�@�i�P�j ����P�̕����Ώیn�̂Ƃ肤���Ԃ́A���ׂ� ��ԃx�N�g���ŕ\�킳��A��ԃx�N�g���̑S�̂͂P�̃x�N�g����Ԃ𐬂��B ��Ԃ͈�ʂɎ��ԂƋ��ɕω�����̂� ��ԃx�N�g���� �������������ԂƋ��ɕς��B
�@�@�i�Q�j ���̕����n�̎��ԓI�ω��́A�n���g�̒��ŋN���镨���I��p�ɂ��A���̍�p�̎d���� ���O�����W�A���܂��̓n�~���g�j�A���ɂ���Č��܂��Ă���B
�@�@�i�R�j ���O�����W�A���A�n�~���g�j�A���� �������i���A���A�Ȃǁj���Ȃ킿 ��p�f �̊�������A��������p�f�͏�ԃx�N�g���̋�Ԃ� �x�N�g���ɍ�p�����B
�@�@�P�̏�ԃx�N�g���ɍ�p�������ʂ��܂� ��ԃx�N�g���ł���B�܂� ��Ԃ� �d�ˍ��킹�̌��������B���������āA��p�f
�@�@�C�ӂ̏�ԃx�N�g���ɑ��āA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@
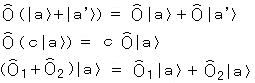
�@�@��p�f�̐�
�@�@�u���x�N�g��
�@�@������p�f
�@�@����ƁA
�@�@�܂��A�@
�@�@�Ō�̎����A���� �u���x�N�g���A�P�b�g�x�N�g���A���`��p�f�̐ς̋���ʂ�����ɂ́A���ꂼ��̋���ʂ����� �t�̏��ł�����Ƃł���B
�@�@��ԃx�N�g���ɍ�p�f����p������� ��ʂɂ͈Ⴄ�x�N�g���ɂȂ邪�A���ʂȏꍇ ���ʂ����Ƃ̃x�N�g���ɕ��f�������������̂ɂȂ�ꍇ������A���̂Ƃ� ���̍�p�f�ɂ���āA�����I��Ԃ͕ω����Ă��Ȃ��B���̂悤�ȃx�N�g���ƌW�������ʂ͕����A���ɂ͖����ɑ��݂���B ���̕��f���̌W���� ��p�f
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�S���������Ƃ� �u���x�N�g���ɑ��Ă����藧�B�@�@�@
�@�@���f�������Ƃ�ƁA�@�@
�@�@�����p�f �p �̋�����p�f�� ���Ƃ̂��̂ɓ������Ƃ��A�p �� ���ȋ�����p�f�i�G���~�[�g��p�f�j�Ƃ����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@���ꂪ�ŗL�l �� �����Ƃ���ƁA�@
�@�@���ӂ̋����́@�@
�@�@�E�ӂ̋����� �@
�@�@���Ȃ킿�@���ȋ�����p�f�̌ŗL�l �� �������ł���B
�@�@�C�ӂ̎��ȋ�����p�f�� �قȂ�ŗL�l�ɑ�����ŗL�x�N�g���� �݂��ɒ�������i�x�N�g�������ς� 0 �j�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E�@����藝�@�@�i�ؖ��j�F
�@�@�@�@
�@�@�� �� �r �Ƃ̓��ς�����ƁA�@
�@�@���������ā@