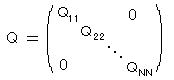２．　複素共役による定式化（２）　・・・観測量の導入（物理化）



　　現実の観測結果に要求される特性は、確率性と実数性がポイントである。
　　物理量は 量子化すると、状態ベクトルに作用する 作用素になり、２．で この性質を調べた。
　　”物理”の理論としては、これらの数学的な量・性質と、”測定値”との関係を与えなければならない。すなわち、古典論と違い、測定装置をも含めた全体の系に 量子力学を適用することを考える必要がある。

　　系が ある物理量を表わす作用素 Ｑ の固有値 ｑ’に属する固有状態にあるなら、その物理量を測定すれば 固有値 ｑ’が得られ、 また逆に、 系が その物理量を測定すると 必ず測定値 ｑ’が得られる状態にあるならば、その状態は Ｑ の固有状態であり ｑ’は固有値である。
　　このとき、物理量は 自己共役作用素 で表わされ、それぞれの固有値（測定値）は実数になる。



　　（１）　固有ベクトル系の展開：


　　対象系の初めの状態 ｌ　〉 は、状態についての重ね合わせの原理から 次のように展開できる。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・　（2−1）
　　初めの状態も、固有状態も １ に規格化し 固有値はすべて異なるとすれば、
　　　　　　　　　　　　　　　　　　　　
　　（3−1）は、すべての状態ベクトルを ある物理量の固有ベクトル系で展開できることを表わし、数学的に言えば ベクトル系の完全性である。すなわち、　　または そのノルムを、ｃｉ を適当にとることによって 0 に収束させることができることである。
　　これを、物理的に言えば、　対象系を一定の条件のもとにある条件に準備し、物理量（運動量、位置、エネルギー、電荷など）を測定する測定装置を作動させ 測定ごとにある決まった値が得られるとすると、この値は物理量の いくつかある固有値のどれかである。　したがって、任意の物理量の固有状態は完全系を表わす。
　　対応する ブラベクトルも同様に展開する。　　　　　　　　・・・　（2−2）



　　（２）　状態ベクトルの確率解釈：


　　 を 自己共役作用素とすると、（2−1）、（2−2）より 　を計算すると、
　　　　
　　（3−1）、（3−2）と 状態ベクトルが規格化されているので、
　　　　　　　　　　　
　　　　　　　　　　　　　　　　∴　　
　　 が １ となるのは、他の ｃｊ がすべて 0 の場合に限る。
　　したがって、物理量の規格化された固有ベクトルで展開したときの係数 ｃｉ は、その絶対値の２乗が 初めの状態で観測したときの測定値 ｏｉ を得る”確率” を与えるものと解釈することができる。（状態ベクトルの確率解釈、　実係数 ｃｉ は改めて”確率振幅”と名づけられる。）

　　状態を ｌ　〉 、作用素を として物理量を測定したとき、個々の測定では 検出される時の状態は ｌ ｉ 〉 （ｉ ＝ 1、2、・・・、ｎ）のどれかになっているから、系の状態は測定によって次のように変化したと考えられる。
　　　　　　　　　　　　　　　　　
　　一方、個々の測定において 巨視的な装置と連動していて古典論的な取り扱いができる場合、量子論的な干渉を示さないから、状態の変化は、
　　　　　　　　　　　　　
　　このような、干渉しないいくつかの状態の集合を、”混合状態”という。
　　（（注）　混合状態の記述は 状態ベクトルではなく 統計作用素によらなければならない。（ →　後述： ＥＰＲ問題））
　　それに対し、状態の重ね合わせができる場合は 状態間の干渉を生じるので、特に区別して、”純粋状態”と呼ぶ。測定によって、このような変化をすることを、状態の収縮、あるいは、波束の収縮と言う。



　　（３）　射影作用素：


　　作用素どおしのベクトル積　 を考えると、任意のケットベクトル ｌ　〉 に対して、
　　　　　　　　　より、
　　 は任意のケットベクトルを ｌ ａ 〉 方向のベクトルにする作用素である。ブラベクトルについても同様である。
　　ある１つの対象系（電子と陽子の束縛系、２電子系など）について、その系がもつ物理量（エネルギー、角運動量など）を Ｏ とし、物理量を表わす自己共役作用素を 、その固有値を ｏ1、ｏ2、・・・、ｏｎ 、対応する規格化された固有状態を ｌ 1 〉、ｌ 2 〉、・・・、ｌ ｎ 〉 とすれば、これらのベクトルは 系のあらゆる状態ベクトルが張る空間で 規格化完全直交系 をつくる。 任意の状態ベクトルは、
　　　　　　　　　　　　　　、　ｃｉ ＝ 〈 ｉ ｌ　〉　　のように展開され、
　　ｃｉ　は ｌ　〉 を ｌ ｉ 〉 方向へ射影した成分（複素数）である。

　　任意の状態ベクトル ｌ Ａ 〉 に対して自己共役作用素　　を考えると、
　　　　　∴　　　　したがって 固有値は ｐＡ’＝ 1 または 0 となり、
　　　ｐＡ’＝ 1 に対応する固有状態は　ｌ Ａ 〉。
　　　ｐＡ’＝ 0 に対応する固有状態は　ｌ Ａ 〉 に直交するすべてのベクトルである。　　を満たす作用素を射影作用素という。
　　自己共役作用素 はその固有ベクトル ｌ ｉ 〉 と 固有値 ｏｉ とを使うと、射影作用素 によって、
　　　　　　　　　　　　　　　　　　　　　　で表わされる。（証明略）

　　２つの自己共役作用素は一般に非可換（積の順を入れ替えて等しくない）であるが、
　　可換なもの　　　　もある。
　　この場合、固有状態を ｌ ｐ’〉 として　 だから、
　　　、すなわち も の固有値 ｐ’に属する固有状態である。このような固有状態が１つしかないとすれば、この固有ベクトルは ｌ ｐ’〉の定数倍しかありえない。
　　すなわち　　　　　　であり、
　　 の固有ベクトルは の固有ベクトルでもある。（２つの物理量の 同時固有状態）　２つ以上の固有状態が同じ固有状態に属しているとき、これらの状態は 縮退している という。固有状態がつくる部分ベクトル空間の中で適当な直交ベクトルを選ぶことによって 同時固有状態を必ず作ることができる。



　　（４）　行列による表示：


　　状態ベクトルのベクトル空間に、直交単位ベクトル系（基底ベクトル）を導入すれば その成分によって表すことができる。基底ベクトル系を、　〈 1 ｌ、〈 2 ｌ、・・・、〈 N ｌ　とすると、任意の状態 ｌ　〉 の各基底ベクトル方向の成分 〈 1 ｌ 　〉、〈 2 ｌ 　〉、・・・、〈 N ｌ 　〉 は ｌ　〉 と１対１に対応する。同様に、〈　ｌ も 〈　 ｌ 1 〉、〈　 ｌ 2 〉、・・・、〈 　ｌ N 〉 と対応する。
　　任意の作用素 は、任意の状態 ｌ A 〉、ｌ B 〉の基底ベクトル ｌ ｉ 〉、ｌ ｊ 〉によって その成分 Ｑｉｊ が、
　　　で表されるので、

　　　　　　　　　　　

　　そこで、Ａｉ ＝ 〈 ｉ ｌ Ａ 〉、 Ｂｊ ＝ 〈 ｊ ｌ Ｂ 〉、 Ｑｉｊ ＝ 〈 ｉ ｌ Ｑ ｌ ｊ 〉 を成分とする行列 Ａ、Ｑ、Ｂ を次のようにとると、
　　　　　　　　　　　　　　　　　　　

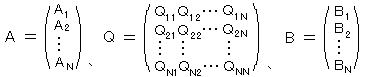
　　たとえば A に、転置行列（行と列を入れ替えたもの）Ｔ 、行列要素を複素共役量としたもの * 、 この両方を行ったもの （エルミート共役）を付けて表すと、　　

　　自己共役作用素のエルミート共役量は、
　より、　　　、　ゆえに、それ自身に等しい。　（エルミート行列）

　　したがって、作用素が自己共役であるとき、行列の対角線要素はすべて実数　 であり、
　　さらに 基底ベクトル系として この作用素の固有状態を選んだとき、　 となって、対角線行列の形になる。
　　　　　　　　　　　　　　　　　　　　

　　　 を満たす行列 Ｕ をユニタリー行列といい、ｐ（運動量）とｑ（座標）の表示の変換に用いられ、交換関係はユニタリー変換によって変わらない。また、自己共役（エルミート）作用素を表す行列は、ユニタリー変換によって対角化できる。（　→　３． ）

　　　　　　　　　　　　　　　次へ　　　　　　　１．へ戻る