丂丂丂丂丂丂丂丂丂丂丂丂俁丏丂晄妋掕惈尨棟丂
丂丂晄妋掕惈娭學偼丄僴僀僛儞儀儖僋偑1927擭偵 兞 慄尠旝嬀偺巚峫幚尡傛傝採彞偟偨傕偺偱偁傞偑丄尰嵼偼丄傎偲傫偳帺慠奅偵偍偗傞婎杮揑側乭尨棟乭偺堦偮偵側偭偰偄傞丅乮傾僀儞僔儏僞僀儞偑惗奤偙傟傪斲掕偟偨偺偼桳柤丅乯丂晄妋掕惈尨棟偼丄娤應慡斒偵偐偐傢傞尨棟偱丄偦偺屻峔抸偝傟偨検巕椡妛偵傛偭偰丄偡傋偰偺惓弨嫟栶側暔棟検偺娫偱惉傝棫偮偙偲偑摫偐傟偨丅奿巕尨巕偺楇揰怳摦丄僗僺儞偺備傜偓側偳偼 偙偺晄妋掕惈娭學偑嬶懱揑偵尰傟傞椺偱偁傞丅
丂丂乮侾乯丂嵗昗昞帵偲塣摦検昞帵丗
丂丂棻巕偺嵗昗丄偁傞偄偼丄塣摦検傪懳妏慄揑偵偡傞昞帵偑旕忢偵傛偔梡偄傜傟傞丅
丂丂偙偙偱丄侾屄偺棻巕偺侾師尦偺塣摦傪憐掕偟乮俁師尦偱傕摨偠偙偲乯丄倯丄倫 傪丄師偺岎姺娭學傪枮偨偡嶌梡慺偲偟偰掕媊偟捈偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丒丒乮3亅1乯
丂丂丂丂鶣乯丂嵗昗 倯 偺屌桳忬懺傪婎掙儀僋僩儖偲偡傞応崌丟
丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂偺傛偆偵摫擖偡傞丅
丂丂屌桳抣 倯乫 偑 亅亣偐傜亄亣傑偱偲傟傞 楢懕屌桳抣側傜偽丄幩塭嶌梡慺偺憤榓
丂丂丂丂丂
丂丂擟堄偺屌桳忬懺 倯乫乫偵懳偟丄丂丂
丂丂捈岎掕棟傛傝丄丂
丂丂偙偙偱丄僨傿儔僢僋偺 兟娭悢乮仏乯 丄偡側傢偪丄
丂丂丂丂丂丂
丂丂乮偨偩偟 倖乮倶乯 偼妸傜偐側娭悢乯 傪摫擖偡傞偲丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂乮3亅2乯丄乮3亅4乯傪枮偨偡屌桳儀僋僩儖宯 倢 倯乫乺 偵偮偄偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂師偵丄
丂丂塃曈 亖
丂丂嵍曈 亖
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亪丂丂
丂丂偙偺椉曈偵 妸傜偐側娭悢 倖乮倯乫乯 傪偐偗偰 倯乫 偱愊暘偡傞偲丄
丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂偱側偗傟偽側傜側偄丅
丂丂偟偨偑偭偰丄擟堄偺忬懺儀僋僩儖 倢丂乺 偺嵗昗昞帵偼丄僔儏儗僨傿儞僈乕偺攇摦娭悢 冋 偦偺傕偺丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偡側傢偪丄丂丂
丂丂乮3亅5乯傛傝丄
丂丂丂
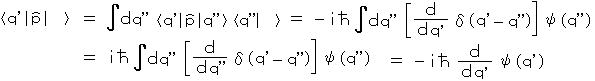 丒丒丒乮3亅6乯
丒丒丒乮3亅6乯丂丂偙偺傛偆偵丄岎姺娭學傛傝丄忬懺儀僋僩儖偺幃偐傜僔儏儗僨傿儞僈乕曽掱幃偑摫偐傟偨丅
丂丂丂丂鶤乯丂塣摦検 倫 偺屌桳忬懺傪婎掙儀僋僩儖偲偡傞応崌丟
丂丂鶣乯偲摨條偵丄倫 偺屌桳忬懺偼丄丂
丂丂峴楍昞帵偼丄丂丂
丂丂岎姺娭學傛傝丄丂
丂丂丂丂丂丂丂丂丂丂丂丂
丂丂塣摦検偺屌桳抣 倫乫 傪傕偮忬懺 倢 倫乫乺 乮塣摦検偑堦掕乯偺嵗昗昞帵偵偍偗傞攇摦娭悢丂
丂丂丂丂
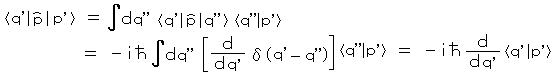
丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亪丂丂丂
丂丂倢 倫乫乺 偼塣摦検偑堦掕偺忬懺乮帺桼棻巕乯偩偐傜丄帺桼棻巕偺嬻娫偵偍偗傞懚嵼妋棪偺怳暆偑 僪丒僽儘僀攇偲堦抳偡傞丅
丂丂枹掕偺娭悢 俠乮倫乫乯 偼丄倢 倫乫乺 傪婯奿壔偡傞偲寛傑傞丗
丂丂丂丂
丂丂偙偺愊暘傪媮傔傞偨傔偵 偁傞妸傜偐側娭悢 倖乮倶乯 偲偦偺 僼乕儕僄曄姺傪丄
丂丂
丂丂忋幃偵戙擖偟偰丄丂
丂丂兟 娭悢偺幃乮3亅3乯偲斾妑偡傞偲丄丂丂
丂丂
丂丂
丂丂嵍曈 亖
丂丂偙傟傪丂塃曈偲斾妑偡傞偲丄丂丂亪丂丂
丂丂乮俀乯丂晄妋掕惈娭學丗
丂丂嘆丂塣摦検偺屌桳忬懺 倢 倫乫乺 傪嵗昗偺屌桳忬懺偱揥奐偡傞偲乮塣摦検偑惓妋偵寛傑偭偰偄傞応崌丗乯丄
丂丂丂丂丂丂丂
丂丂偙偺忬懺偱丄塃曈偺倢 倯乫乺 偺學悢偼丄棻巕偺埵抲偑 倯乫偐傜 倯乫亄 倓倯 偵偁傞妋棪 俹p乫乮倯乫乯倓倯乫 傪梌偊傞妋棪怳暆偩偐傜丄丂
丂丂嘇丂嵗昗堦掕偺忬懺 倢 倯乫乺 傪塣摦検偺屌桳忬懺偱揥奐偡傞偲乮埵抲偑惓妋偵寛傑偭偰偄傞応崌丗乯丄
丂丂丂丂丂丂丂
丂丂學悢偼 塣摦検偑 倫乫偐傜 倫乫亄 倓倫乫 偵偁傞妋棪 俹倯乫乮倫乫乯倓倫乫 傪梌偊傞妋棪怳暆偩偐傜丄丂
丂丂嘊丂偝偰丄 尰幚偺応崌丄偨偲偊偽 幚尡幒揑側僄僱儖僊乕儗儀儖偺棻巕慄偼丄塣摦検偼拞怱抣偺傑傢傝偵 侾亾掱搙偺峀偑傝偑偁傝丄偦偺嬻娫揑側峀偑傝偼 悢們倣掱搙偱偁傞丅偙偺傛偆偵丄堦斒偵丄塣摦検偲埵抲偼 暘晍傪傕偭偰偦偺峀偑傝偑懚嵼偟丄棻巕偼 攇懇 偺忬懺偱偁傞丅
丂丂侾師尦偺侾屄偺棻巕傪峫偊丄埵抲偺峀偑傝偑暆 嚈倯 偱梌偊傜傟偰偄傞攇懇偱偁傝丄暯嬒偺埵抲偺嵗昗傪尨揰偵偲傝丄恑峴曽岦偵 僈僂僗宆偺暘晍乮暆 嚈倯 偼昗弨曃嵎 亖 冃 乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂攇懇偺忬懺儀僋僩儖傪 倢 倂 乺 偲偡傞偲丄嵗昗偺屌桳抣偑 倯乫 偱偁傞傛偆側忬懺 倢 倯乫乺 偱揥奐偟偨偲偒偺妋棪怳暆偼丄
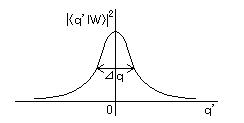
丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丒丒乮3亅9乯
丂丂偲偍偗傞丅丂俠倂倯 偼暋慺悢偺掕悢偱丄偦偺愨懳抣偼丄
丂丂
丂丂僈僂僗愊暘偺岞幃丂
丂丂丂丂丂丂丂丂丂
丂丂偙偺忬懺偵偍偄偰 塣摦検
丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂
丂丂巜悢娭悢偺巜悢偼 倯乫偺崁偱暘偗丄
丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂偙傟偼乮3亅9乯偲摨偠宍側偺偱丄
丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂偲彂偗傞丅
丂丂乮3亅11乯偲乮3亅12乯偺檖傪斾妑偡傞偲丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亪丂丂
丂丂偡側傢偪丄丂桳柤側 僴僀僛儞儀儖僋偺晄妋掕惈娭學偺幃偑摫偐傟傞丅
丂丂偁傞偄偼丄乮3亅11乯丄乮3亅12乯偺學悢傪斾妑偡傞偙偲偵傛偭偰傕摼傜傟傞丅丂俠倂倫 偼乮3亅10乯偲摨條偵丄
丂丂丂丂丂丂丂
丂丂偙偺傛偆偵丄偁傞暔棟検偑屳偄偵旕壜姺偱偁傞側傜偽丄偦傟傜偺娫偵偼 晄妋掕惈娭學偑偁傝丄偦偺嬶懱揑側宍偼 惓弨嫟栶側嵗昗偲塣摦検偺娫偺 岎姺娭學偐傜寛傑傞丅
丂丂仏丂丂僨傿儔僢僋偺 兟娭悢丗
丂丂丂丂丂丂
丂丂偨偩偟丄倖乮 倶 乯 偼妸傜偐側娭悢丅丂兟娭悢偼挻娭悢偺堦偮偱丄偦傟帺恎偱偼堄枴傪帩偨偢 倖乮 倶 乯 偲偺愊偺愊暘偺宍偱梡偄傜傟傞丅丂兟娭悢偺惈幙傪嫇偘傞偲丄
丂丂丂丂丂丂丂
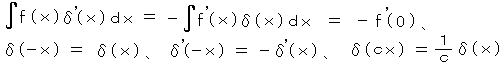
丂丂乮俁乯丂儐僯僞儕乕曄姺丗
丂丂俀丏乮係乯偵偍偄偰丄壜姺側 暔棟検偺姰慡宯偺屌桳忬懺傪梡偄偰丄忬懺偲嶌梡慺傪昞尰偟偨丅
丂丂偝傜偵丄傕偭偲堦斒揑偵丄俀偮偺旕壜姺側暔棟検
丂丂俻1丄俻2丄丒丒丒丄俻俶丟丂倢 俻1 乺丄倢 俻2 乺丄丒丒丒丄倢 俻俶 乺丟丂俹1丄俹2丄丒丒丒丄俹俶丟丂倢 俹1 乺丄倢 俹2 乺丄丒丒丒丄倢 俹俶 乺丂偲偍偔丅丂丂擟堄偺忬懺 倢丂乺 偵懳偟丄俻 昞帵 乹 俻倝 倢丂 乺 偲 俹 昞帵 乹 俹倞 倢丂 乺 偲偺娫偵偼丄
丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
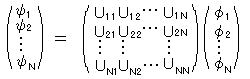 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丒乮3亅14乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丒乮3亅14乯丂丂揮抲峴楍傪
丂丂丂丂丂丂
丂丂峴楍 倀 偼丄丂丂
丂丂俻 昞帵丄俹 昞帵偺曄姺傪 儐僯僞儕乕曄姺偲屇傇丅
丂丂嶌梡慺
丂丂丂丂丂丂丂丂
丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂偲彂偗傞丅
丂丂屳偄偵惓弨嫟栶側嵗昗偲塣摦検偺岎姺娭學丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
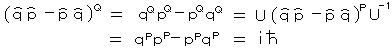
丂丂偲側偭偰丄岎姺娭學偼儐僯僞儕乕曄姺偵傛偭偰曄傢傜側偄丅
丂丂乮係乯丂忬懺偺帪娫敪揥丗
丂丂検巕椡妛偺妋棪揑尰徾偺攚屻偵偼丄廳偹崌傢偣偺尨棟傪枮偨偡 忬懺儀僋僩儖偑懚嵼偟丄偙傟偑 帪娫揑偵堦堄揑偵曄壔偡傞偲峫偊傜傟傞丅帪崗 倲 偵偍偗傞忬懺儀僋僩儖傪丂倢 俙丄倲 乺丄倲 傛傝枹棃偺帪崗 倲乫 偵偍偗傞忬懺儀僋僩儖傪 倢 俙丄倲乫乺 偲偡傞偲丄倢 俙丄倲乫乺 偼 倢 俙丄倲 乺 偵傛偭偰寛偭偰偄傞偼偢偱偁傞丅
丂丂廳偹崌傢偣偺尨棟偵傛傝丄
丂丂丂丂丂丂丂丂丂丂
丂丂廳偹崌傢偣偺尨棟偑宲懕偡傞偨傔偵 偙偺娭學偼 擟堄偺帪崗 倲乫
丂丂丂丂丂丂丂丂丂丂
丂丂偙偺娭學傪 慄宍嶌梡慺傪巊偭偰昞偡偲丄
丂丂摨條偵丄丂丂丂丂丂丂丂丂丂
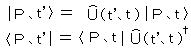 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丒丒乮3亅16乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丒丒乮3亅16乯丂丂偲側傝丄
丂丂帪崗 倲乫 偵偍偗傞儌乕僪 俹 偺懚嵼妋棪 偼丄
丂丂
丂丂擟堄偺 倲丄 倲乫 偵懳偟丄
丂丂丂丂丂丂丂丂丂丂
丂丂偱偁傝丄
丂丂偟偨偑偭偰丄偡傋偰偺忬懺偺帪娫敪揥偼丄乮3亅16乯偵廬偭偰儐僯僞儕乕偵峴傢傟傞丅
丂丂桳尷偺帪娫娫妘偵偍偗傞帪娫敪揥偼丄柍尷彫偺帪娫娫妘偵偍偗傞曄壔偺愊傒廳偹偱偁傞偲偡傞丅乮偙傟偼嬤愙嶌梡偺尨棟偲傕娭學偟偰偄傞丅乯丂倲乫 偑 倲 偵柍尷偵嬤偄嬌尷傪峫偊傞偲丄
丂丂丂丂丂丂
丂丂偙偙偱丄
丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亪丂
丂丂偙傟傪梡偄偰丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂傛傝丄柍尷彫偺帪娫敪揥傪昞偡嶌梡慺偵側偭偰偄傞丅
丂丂乮3亅7乯偺傛偆偵丄丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂
丂丂偲側偭偰丄俫 傪僴儈儖僩僯傾儞偲偡傞偲 偙偺幃偼丄 僔儏儗僨傿儞僈亅曽掱幃
丂丂丂丂丂丂丂丂