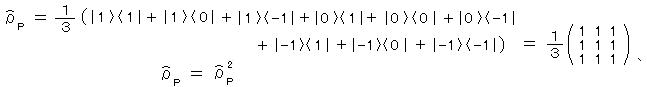４． 混合状態と統計作用素：
（１） 純粋状態と混合状態：
電子は、スピン角運動量
をもち、ある方向への成分 
（ｚ 軸成分とする）の固有値は、 
だけが可能である。 電子線のスピン状態 は、
となる ｌ α 〉、ｌ β 〉 の張る空間で表すことができる。スピン状態が、
で表されるとすると、 行列表現
より 
となり １ に規格化されている。 また、状態ベクトルの固有値による展開式は 
・・（3－4） で、 ｉ 番目の固有値が与えられる確率は 
になる。したがって、状態 ｌ χ＋〉 にある電子のスピンを測定したとき
となる確率は、それぞれ １/２ となる。 この確率は、波動関数を 
と書いても同じである。ｌ χ＋〉、ｌ χ－〉 は ｚ 成分だけを測定しても区別がつかないが、 ｘ 軸成分 の測定値によって それらを区別することができる。
によっても、 ｌ χ±〉 は ｘ 成分の固有値 
の固有状態である。ｎ を （ｘ、ｙ、ｚ） ＝ （ｃｏｓθ、ｓｉｎ θ、0）の単位ベクトルとすると、
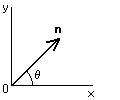
（θ は任意の実数） は、スピン成分
の固有値 
の固有状態となっている。そして、 χθ の状態でスピンの ｚ 成分を測定すれば、 を得る確率も それぞれ １/２ である。さて、以上は １つの線源からの電子線についてであったが、ここで、２つの異なる線源から１つに合成した電子線は、それぞれの線源の固有状態
の強度を同じにつくっても、 位相 ｅｘｐ（ｉθ） は全く乱雑である。この場合、スピンの ｚ 成分を測ると 確率はそれぞれ １/２ であるが、ある物理量の固有状態にはなっていない。このような、１つの状態ベクトルで表せない状態を、”混合状態”と言う。（ＥＰＲ問題はこの例）一方、１つの線源からの電子線（２つに分けてから１つに再合成した場合も含む）は、
、
、
において展開した 基底ベクトル ｌ α 〉 と ｌ β 〉 との間の位相が、 の場合 １、 の場合 －１、 の場合 
であり、
のように 重ね合わせの原理によって １つの状態ベクトルをつくる。これを、特に区別して ”純粋状態”と呼ぶ。（２スリット実験、遅延選択実験など） 今までの議論で扱ってきた
状態ベクトルで表せる状態は すべて純粋状態である。加速器実験で一定の運動量に加速して作られる粒子のスピン状態は 通常 乱雑である。（計算ではスピン状態を平均したものを実験と比べる。） 磁場などで スピンをある割合まで一定方向に整列させる実験を、”偏極実験”と言う。
スピンに依存するある物理量
の、１つの純粋状態 における期待値は、
であり、 ｅｘｐ 部が干渉効果（量子力学的干渉）を表し、状態
において 物理量 を測定したときの平均値となる。これは、状態 ｌ α 〉 と ｌ β 〉が同数ずつ混在している場合の単純な平均 
ではない。（２） 統計作用素：
１つの作用素
の 状態 ｌ Ａ 〉 における期待値 
は 任意の 規格化直交完全系 ｌ ｉ 〉を用いて、
ここで、
を の 対角和（トレース）と言い 行列の対角線要素の和であり、 だけによって決まる。状態が混合状態であるとは、純粋状態 ｌ Ａ 〉、ｌ Ｂ 〉、ｌ Ｃ 〉、・・・ の混合であり、それぞれの混合の確率を Ｗ（Ａ）、Ｗ（Ｂ）、Ｗ（Ｃ）、・・・ とする。 物理量
の状態 ｌ Ａ 〉 における期待値は 
だから、 混合状態での の平均値は、
直交完全系 ｌ ｉ 〉 を用いて、
ここで、
・・・・・（4－1）は、それぞれの純粋状態への射影作用素に その状態が含まれる確率 を掛けたものの和であり、これを ”統計作用素”（または 密度行列）と呼ぶ。統計作用素は自己共役作用素である。
より、
の対角和をつくると、
。 
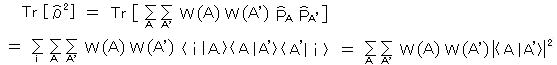
が成り立つのは、すべての状態 ｌ Ａ 〉、ｌ Ｂ 〉、ｌ Ｃ 〉、・・・ が 同じ物理的状態の場合である。ここで、 純粋状態は、 （4－1）で Ｗ（Ａ） のうち１つだけ１ たとえば Ｗ（Ａ） ＝１ で他は 0 の場合だから、
したがって、 純粋状態のとき
また、 混合状態のとき
・・・・・・（4－2）であり、これは 純粋常態か混合状態かの判別に用いられる。
の運動方程式は、状態ベクトルに対する運動方程式
から与えられる。この共役な式は 
である。これらにより、
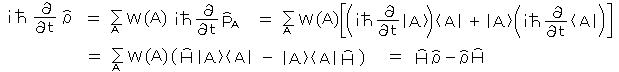
したがって、統計作用素の運動方程式は、
で与えられる。
ユニタリー作用素 （3－16）
より、
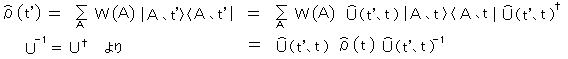
すなわち
、、
、
の時間発展は ユニタリー変換によって変わらない。したがって、（4－2）より、 閉じた系が 純粋状態ならばいつまでも純粋状態で、混合状態ならばいつまでも混合状態である。
（３） 部分系：
水素原子は その部分系である 陽子と電子から成っている。原子核では Ｚ 個の陽子と Ａ － Ｚ 個の中性子が それぞれ部分系である。 量子力学においては、現象の背後に 状態ベクトルと統計作用素を考えるため、全系と部分系との関係は 特に考慮されなければならない。
簡単のため、それぞれが スピン １/２ の粒子である ２つの部分系から成る系を考える。
スピン角運動量がそれぞれ
、
をもつ２つの粒子のスピン角運動量を合成すると、
とおける。
の固有値を 
とすると、 Ｓ ＝ 0 または １ である。① Ｓ ＝ 0 のときの状態：
（一重状態）② Ｓ ＝ １ のときの状態：
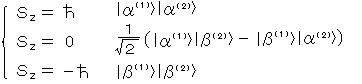（三重状態）それぞれの部分系の状態ベクトルは、 ｌα（ｉ）〉、ｌβ（ｉ）〉 （ ｉ ＝ 1、2） の１次結合で、
また、全系の任意の状態ベクトルは、 ｌα（1）〉ｌα（2）〉、 ｌα（1）〉ｌβ（2）〉、 ｌβ（1）〉ｌα（2）〉、 ｌβ（1）〉ｌβ（2）〉 の１次結合（重ね合わせの原理の１つの具体例）で表される。
① 全系のスピンが 0 のときの、スピンに関する状態ベクトルは、
であり、１番目、２番目の粒子のスピンの ｚ 成分を測定して ＋１/２ あるいは －１/２ を得る確率は それぞれ ５０％である。
（ ＊ １個の電子スピンの状態は、
で表され、これは ｚ 成分 が 上向き と 下向き の状態の１：１の重ね合せを意味する。このとき、スピンの ｚ 成分を測定すれば ＋１/２、－１/２
を得る確率は それぞれ ５０％である。一方、スピンの ｘ 成分 を測定した場合 １００％の確率で ＋１/２ を得る。このように、上向き・下向きの言葉が、状態か、測定結果か で、意味が全く違うことに注意。）
２粒子をそれぞれの部分系とする系の それぞれの状態を表す直交完全系として、 ｌα（1）〉ｌα（2）〉、 ｌα（1）〉ｌβ（2）〉、 ｌβ（1）〉ｌα（2）〉、 ｌβ（1）〉ｌβ（2）〉 をとることができる。それぞれは、部分系 １ の状態と 部分系 ２ の状態との積であるが、量子力学的干渉は現れない。
しかし、それらの１次結合
などには 量子力学的干渉が現れる。全系の、この状態の統計作用素は、ブラベクトルをかけて、
・・・・（4－3）粒子の相手が違う場合で分けると、（１ は １ どおし、２ は ２ どおし；
記号は 直積）
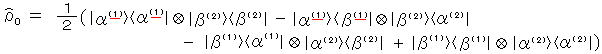
ｌ 1 〉 ＝ ｌα（1）〉ｌα（2）〉、 ｌ 2 〉 ＝ ｌα（1）〉ｌβ（2）〉、 ｌ 3 〉 ＝ ｌβ（1）〉ｌα（2）〉、ｌ 4 〉 ＝ ｌβ（1）〉ｌβ（2）〉 （直交完全系） として
（ｉ、ｊ ＝ 1、2、3、4） を計算すると、
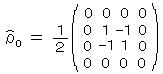となって、エルミート行列 
になっている。これは、
であるから、純粋状態を表している。ここで、部分系・粒子 １ の状態でつくる空間で作用する作用素
を求める。部分系 １ のある物理量
を測定する場合、対象系は全系であるから、作用素は
であり、その期待値は、
とおくと、これは部分系 １ の状態のつくる空間で作用する作用素で、
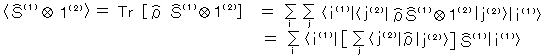
と書ける。したがって、（4－3）を使って
の全スピンが 0 である系について計算すると、
∴
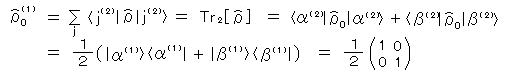
となって、
は 部分系 １ について、スピンの ｚ 成分の上向き状態 ｌα（1）〉 と下向き状態 ｌβ（1）〉 とが １：１ に混じった 混合状態 を表す。このように、全系が１つの純粋状態にある場合でも、その部分系は、一般に、混合状態である。
② また、２個の粒子から成る系が スピン １ の状態にある場合は、
ⅰ） スピンの ｚ成分 の３つの固有状態が 同じ割合で混合しているとき、
ⅱ） スピンの ｚ 成分 の３つの固有状態が １：１：１ に重ね合わされているとき、
より、