５． ＥＰＲ問題とその解決
１９３５年に アインシュタイン（Einstein）、ポドルスキー（Podolsky）、ローゼン（Rosen）の３人は、波動関数 あるいは 状態ベクトルによる物理的実在の記述の不完全性（パラドックスを生じる）について問題提起した。（３人の頭文字を取ってＥＰＲパラドックスという）
（１） ＥＰＲパラドックス：
全スピンが 0 の束縛状態（ポジトロニウムの基底状態（電子と陽電子の束縛状態）など）にある、２個のスピン１/２の粒子について考察する。
初めのスピン状態は、
（ ｌ α 〉、ｌ β 〉 はスピンの ｚ 成分が ＋１/２、−１/２ の固有状態）で記述される。時刻 ｔ0 に２粒子の束縛状態が壊れ、そのスピン状態はそのままで、２粒子は反対方向（ｙ 軸方向）へ飛び出すとする。その後 時刻 ｔ1 に 片方の粒子が 不均一磁場を通ってスピン方向によって分離され検出器に入るものとする。（シュテルン・ゲルラッハの装置） このとき、粒子 １ の情報は、粒子 ２ がどんなに離れていても、粒子 ２ のスピン方向の情報をただちに与える。このこと自体には何ら矛盾はなく、相関は角運動量の保存則から出たもので、ごくあたりまえの結果である。
パラドックスは、状態ベクトルが自然を記述するとこから起こる。
測定が行われた時刻 ｔ1 より未来において、粒子 ２ の状態ベクトルは、
となる。粒子 ２ は ｔ0 より後にはまわりから何の影響も受けておらず、粒子 １ の測定は、粒子 ２ に何の影響も及ぼさないはずである。 したがって、
となって、粒子 ２ のスピンの方向は初めからずっと変わっていない。 このことは、初めの状態、
では、 であり、 初めの状態がこの式で表されることはいろいろな方法で認められているから、ｌ α 〉（＋１/２） も ｌ β 〉（−１/２）も含まれている。 すなわち、粒子 ２ の状態は、粒子 １ の状態を測定したとき変わることになる。 この変化は、粒子間の距離がどんなに離れていても、何の物理的作用もないのに起こる奇妙なものである。次に、測定装置を９０°回転して、スピンの ｘ 成分を測定すると、同様に 初めの状態は スピン 0
である。粒子 １ を測定したときのスピンの ｘ 成分を
とすると、 
より、 時刻 ｔ1 において 粒子 １ のスピンの ｘ 成分を測定すると、 ＋１/２ であるなら 粒子
２ は−１/２ である。ゆえに、
であり、また、 
であり、ｘ 成分においても 初めから変わっていない。 ところが、ｚ 成分の測定では
であった。このように、測定を行う前の状態に対し、未来に何を測定するかによって、異なる２つの答えが与えられる事になり、これはパラドックスである。
（２） 統計作用素の記述によるパラドックスの解消：
（１）の考察には問題を含む。 すなわち、 測定過程は、スピンに関する純粋状態から混合状態への変化であり、少なくとも ｔ ＜ ｔ1 において ２粒子は全体として１つの系を成しており、粒子 ２ はその部分系だから ｔ1 ＞ ｔ ＞ ｔ0 の状態は １つの状態ベクトルで記述することができず 統計作用素によらなければならない、ということである。
系の初めの状態は、
であり、 その統計作用素は、
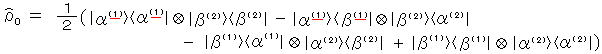
であり、 その行列表示は、スピンの ｚ 成分を対角線的にする表示、
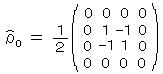で与えられる。純粋状態から混合状態になるということは、量子力学的干渉が測定過程で消えることを意味し、
と表現される。測定後、対角線部分に残っている ｌα（1）〉ｌβ（2）〉、 ｌβ（1）〉ｌα（2）〉 は、 スピンの ｚ 成分が 粒子 １ が下向きならば 粒子 ２ は上向き、１ が上向きならば ２ は下向き であることを示す。 測定値は個々の場合には予測できず、それぞれの確率は １/２ であると言えるだけである。
ここで、測定後の粒子 ２ の状態は、粒子 １ の部分対角和をとったものなので、
より、
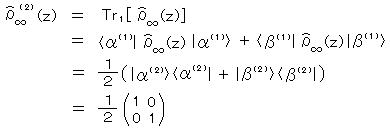となる。これを 測定前の 粒子 ２ の状態と比較すると、
より、
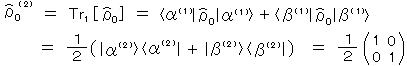
となって、測定後と全く同じである。すなわち、部分系である粒子 ２ の状態は、粒子 １ の測定によって何の変化も受けない。
また、スピンの ｘ 成分 について、粒子 １ のスピンを測定した場合の 初めの状態ベクトルは、
であり、 統計作用素の変化は、
粒子 １ のスピンを測定した後と、測定前の 粒子 ２ の状態は、それぞれ、
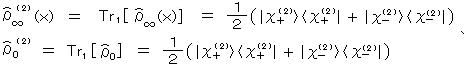であり、やはり、
となって、 ｘ 成分についても、粒子 ２ の状態は、粒子 １ の測定によって変わらない。