３－2 ラプラス方程式の導出
ラプラス方程式（その解は調和関数）は、コーシー・リーマンの関係式（ｕ と ｖ は”調和共役”という）を微分して得られ、これと全く等価である。（さらに ５－3 で述べる コーシーの第１積分定理とも同等である。） したがって、あらゆる 正則関数（解析的な関数）の実部、虚部のそれぞれは、ラプラス方程式の解である。
正則性を表す一つの形である ラプラス方程式の特徴は、人間の直感（物理法則）を盛り込みやすい形式であり、これは 物理学起源の多くの主要なテーマを それぞれの理論の出発点になるほどに 非常にきれいな形で表現するものである。（”空間的表現”（ラプラス方程式） ＋ 他の物理的要因の形で。 ただし、ラプラス方程式に何かをくっつけた式の解には 正則でない解も含まれる。（シュレディンガー方程式の”複素共役”な波動関数の解など））
また、微分方程式を解くことは一般的に非常に難しい。それらの方程式の解には、正則関数の代表である指数関数（ｅｘｐ 関数）が 常に ”基本解” として独占的に現われている。これは 思索的に直感する、というのではなく、特殊解として指数関数を初めから想定して、式に当てはめてみて確かにそうであると知る、という思索の展開の流れである。（「初めに ことば があった」）
・・・ 神の３定数（ｅ 、π、ｉ ）による”キリスト”関数（キリスト＝油（ ｉ ）注がれた者（ ｅ ））は、自然の摂理を根底からあかしする！
（１） コーシー・リーマンの関係式の導出：
関数の正則性・・・どの方向から微分しても同じ値になる・・・を評価する コーシー・リーマンの関係式は、複素関数についての微分の定義式から簡単に求められる。
複素関数 ｆ（ｚ） について ｚ0 における微分を求めると、
１） ｘ 軸から近づけると、
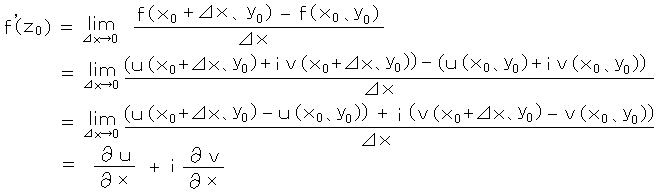
２） ｉ ｙ 軸から近づけると、
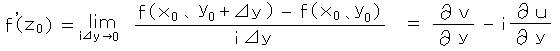
１）＝２）で 実部 と 虚部 を それぞれ 等値とおくと、 コーシー・リーマンの関係式
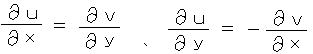が得られる。ｘ 軸、ｉ ｙ 軸から近づけて同じならば、どの方向から近づけても同じになる。
ｅｘ） ・ 共役複素数への写像 ｆ（ｚ） ＝ ｚ* ＝ ｘ － ｉ ｙ （すなわち、ｕ ＝ ｘ 、 ｖ ＝ －ｙ ） では、
となって 満たさないので、これは 複素平面のどの領域でも正則でない。・ また、実数部のみを対応させる写像も 全面で正則でない。
（２） ラプラスの方程式の導出：
コーシー・リーマンの関係式を それぞれ ｘ と ｙ で 偏微分すると、
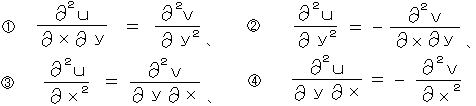
②と③より、また ①と④より、それぞれ ｕ と ｖ （どちらも 実関数）についての 二次元の ラプラス方程式が導かれる。
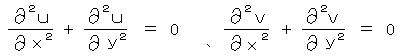
ここで、
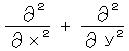を 演算子として、 
・・・ ラプラシアン と書き、 
のように表すことが多い。 ただし 
三次元の場合は、
となる。三次元のラプラシアンの極座標表示は、
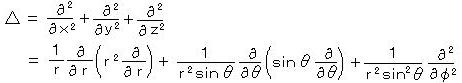
で与えられる。
（３） ラプラス方程式の適用：
ラプラス方程式そのものは ベクトル場のポテンシャルを記述し、この式（右辺 ＝ 0）だけで 様々な物理的なポテンシャルを表わすことができる。（たとえば、非圧縮性の流体の定常流、熱伝導体の定常温度分布、重力や静電場、時刻 ｔ に関係しない定常状態（永遠の状態）など。） これに、さらに 関数や時間微分、他のベクトル場のポテンシャルなどを付け加えることによって 各種の物理的な意味付けがなされ、物理学と工学の諸分野において それぞれの理論の中心ポイント（理論の出発の式）を表す方程式として用いられる。
物理学、工学でよく用いられる 偏微分方程式（常微分方程式よりも 解の集合の範囲が大きい）には 次のような形式があり、ラプラス方程式が基本形になっている。
１） ラプラス方程式；
・・・ φ を 電場ポテンシャル Ｖ ととって 他の電荷の無い静電場、 重力場ポテンシャル など。解は すべて正則関数。
２） ポアソン方程式；
ｆ は既知の関数 あるいは 定数・・・ φ を電場 Ｖ、 ｆ を粒子の電荷密度 にとって 電荷の存在する静電場ポテンシャル
、質量の存在する重力場 など。３） 熱方程式；
・・・ ｕ を温度 Ｔ 、 ｋ を熱拡散率（λ/Ｃｖ）とすると、時間とともに変化する温度分布が得られ、時間と共に均一になる。
４） 波動方程式；
・・・ 光、音、弦や膜の振動などの波を表現し（ ｃ は 波動の伝播速度）、波動方程式の解は正弦波を重ね合わせることにより得られる。
５） 調和振動子（シュレディンガーの方程式）；
ⅰ） 一次元のバネの場合（単振動の定常振動）；
・・・ 調和振動子は 数学的には ポアソン方程式の一つで、特に 関数 ｆ にポテンシャルを追加したもので、中心力場のモデルである。ポテンシャルの大きさが 距離の２乗に比例する理想的なバネを想定すると、バネ定数を ｋ とする振動子は バネの復元力 Ｆ ＝ － ｋ ｘ （変位に比例）より、 変位 ｘ における エネルギー・ポテンシャルは
。 解の満たす条件（① 変位の絶対値に対し等しい運動になる、② 変位が∞になるとき
0 になる）から、 
が一つの解（特殊解）として与えられ、 級数展開によって一般解が求められる。ⅱ） 三次元の定常波で クーロン力によるポテンシャルに束縛された系（水素原子）；
・・・ 陽子による ポテンシャル
に束縛された電子の時間によらない波動を表現し、これを解くことによって
各量子数 （ｎ、ｍ、ｌ ）ごとの 電子の確率分布が導出される。ただし ⅰ）のようなバネと違って、ポテンシャルＶは
無限遠点で 0 にするため 調和振動子ではない。たとえば 磁気量子数 ｍ は、極座標で表示し Ｒ、Θ、Φ が変数分離された
が、0 ～ ２π で規格化され、
ここで、Φ は φ についての周期 ２πの多価関数
である事から、解の一価性より、ｍ ＝ 0、±１、±２、・・・・ （磁気量子数） のどれかを選択する。
このように、自然の量子性（不連続性）は 解である 指数関数の多価性から出ている！。
ｍ から ｌ、ｎ が決定され、逆に、ｎ が定まると、ｌ、 そして ｍ の上限値・下限値が自動的に決まる。
・・・・・・ 以上は、線形（＊）偏微分方程式 で、 ｅｘｐ 関数を基本とするきれいな形の解を持つ。
６） 非線型の偏微分方程式の例；
ⅰ） 粘性流体方程式（ナビエ・ストークスの式）；
（注：この式は 未だ 他の物理法則から導かれていない 経験則） 左辺は 運動量の時間的・空間的変化（結果）を、（ρ 密度、ｕ 速度ベクトル） 右辺は 圧力（ ｐ ）と粘性（μ）による運動量輸送（各要因）を表わす。 左辺の ｕ・∇ｕ の項（移流項）は強い非線形性を持ち、これによる 乱流の非定常性を発生させる要因を、 右辺の μの項（粘性項）が抑制する形であり、乱流発生の しきい値を決めるのに レイノルズ数（Ｒｅ ＝ Ｕ Ｌ/（μ/ρ） ・・ 無次元数、（Ｕ 特性速度、Ｌ 特性長さ））が用いられる。
ⅱ） アインシュタインの重力場方程式；
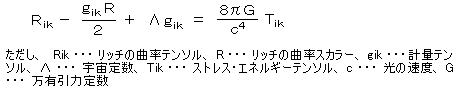
・・・ 一般相対性理論によれば、重力場は時空の曲がりと等価であり、その正しさは、多くの天体現象や素粒子の現象で確認されている。 この式の 左辺は 時空の幾何学的曲がり、右辺は 物質場（質量またはエネルギー）。 ｇｉｋ は 多様体の計量を記述し、１０個の独立成分を持つ ４×４ の対称テンソル。４つの時空座標についての選択の自由があるので 独立した方程式は ６つになる。
宇宙項については一時撤回されたが、近年宇宙がわずかに加速度的に膨張している観測結果より 再び見直されている。