丂丂丂丂丂丂丂俁丏丂巜悢娭悢傊偺暋慺悢偺摫擖
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俁亅2丂儔僾儔僗曽掱幃
丂幚幉偲嫊幉偱峔惉偝傟傞乭暯柺偺悢乭丒丒丒暋慺悢偙偦偑丄巚嶕丄偍傛傃丄帺慠奅偺彅尰徾乮摿偵丄検巕椡妛乯傪昞尰偡傞偨傔偺悢偺杮幙偱偁傞丅暋慺悢偺応偵偁偭偰偼丄倕 偺巜悢娭悢乮倕倶倫 娭悢乯偺傒偑帺桼偵夝愅揑側怳晳偄傪峴偆偙偲偑偱偒傞傛偆偵惗偒巆偭偰偄傞丅偦偟偰偦偺昡壙偵丄娭悢偑乭惓懃乭偱偁傞偐偳偆偐偑梌偊傜傟偰偄傞丅惓懃惈偼丄暋慺娭悢傪峫偊傞帪偺乭棩朄乭偺傛偆側惂尷帠崁偱偁傞丅
丂暋慺暯柺忋偱掕媊偝傟偨娭悢偵偮偄偰丄師偺俀忦審丄侾丏旝暘壜擻丄俀丏僐乕僔乕丒儕乕儅儞偺娭學幃丄傪枮偨偡帪丄偦偺娭悢偼乭惓懃娭悢乭乮夝愅揑側帺桼傪帩偮乭惓摑側乭娭悢乯偲屇傇丅
丂乭惍幃乭丄乭桳棟幃乮惍幃偳偍偟偺暘悢宍乯乭偱昞偝傟傞娭悢偼丄偡傋偰惓懃偱偁傞丅偙偙偱丄惍幃偺師悢傪柍尷偵崅傔偰奼挘偟偨丄乭傋偒媺悢乭傕丄廂懇偡傞斖埻撪偱惓懃娭悢偱偁傝丄偦傟埲奜偵偼柍偄丅
丂乮偨偲偊偽丄暋慺悢偺幚悢晹暘偺傒偵懳墳偡傞幨憸乮倸 仺 倶乯偼惓懃偱側偄丅丂倕倶乯 帺慠偺杮幙偼暋慺悢偱偁傞丅検巕椡妛偵偍偄偰丄揹巕偺攇摦偺姳徛偵傛偭偰娤應偵尰傟傞憸乮暋慺悢偺攇摦娭悢偺乭幚悢晹暘乭乯偑妋棪揑偱偁傞帠偲娭楢偟偰偄傞丠乯
丂倕 偺巜悢娭悢傗嶰妏娭悢偼丄僥乕儔乕揥奐乮倶 亖 侽 偺帪儅僋儘乕儕儞揥奐偲傕尵偆乯偵傛偭偰傋偒媺悢偵揥奐偝傟丄偦傟偧傟偺曄悢偵暋慺悢 倸 亖 倶 亄 倝 倷 偑摫擖偝傟 丄倕倶倫 倸 側偳偑掕媊偝傟傞峔憿偵側偭偰偄傞丅
丂偙偺傛偆偵偟偰掕媊偝傟偨暋慺悢偺巜悢娭悢偵傕幚悢偲摨偠傛偆偵丄
丂丂丂丂丂侾丏旝暘偟偰傕曄傢傜側偄惈幙丂乮倕倶倫 倸乯乫亖 倕倶倫 倸
丂丂丂丂丂俀丏巜悢朄懃丂倕倶倫乮倸1亄倸2乯亖倕倶倫 倸1 亄 倕倶倫 倸2丂偑惉傝棫偮丅
丂巜悢朄懃偵傛傝丄暋慺悢傪幚晹偲嫊晹偱暘偗傞偲丄桳柤側丄僆僀儔乕偺岞幃丂
丂丂丂丂丂丂丂丂倕倶倫 乮倸乯 亖 倕倶倫 乮倶 亄 倝 倷乯 亖 倕倶倫 倶 丒乮們倧倱 倷 亄 倝 倱倝値 倷乯
偵側傞丅 丂倸 偑弮嫊悢 倝 倶 偺応崌丄僆僀儔乕偺娭學幃丂丂倕倶倫乮倝 倶乯 亖 們倧倱 倶 亄 倝 倱倝値 倶 丂偲側傞丅
丂丂乮侾乯丂丂惓懃娭悢丗
丂暋慺暯柺丂俢乮倶 丄倝 倷乯忋偱掕媊偝傟偨幚悢抣娭悢 倳乮倶丄倷乯丄倴乮倶丄倷乯偵偮偄偰丄
丂丂丂丂丂丂丂侾丏丂倳乮倶丄倷乯丄倴乮倶丄倷乯偼偲傕偵丄旝暘壜擻
丂丂丂丂丂丂丂俀丏丂僐乕僔乕丒儕乕儅儞偺娭學幃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
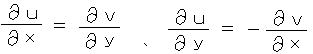 丂傪枮偨偡帪丄
丂傪枮偨偡帪丄丂丂丂丂丂丂丂倖乮倸乯 亖 倳乮倶丄倷乯丂亄丂倝 倴乮倶丄倷乯丂丄丂倸 亖 倶 亄 倝 倷丂偲偍偔偲丄
丂丂丂丂丂丂丂倖乮倸乯偼 俢忋偱惓懃娭悢偱偁傞偲尵偆丅
丂丂僐乕僔乕丒儕乕儅儞偺曽掱幃偼丄旝暘傪偳偺曽岦偐傜嬤偯偗偰峴側偭偰傕摨偠抣偵側傞忦審傪尵偭偰偄傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮摫偒曽丗仺 俁亅2乯
丂丂倖乮倸乯丄倗乮倸乯 偑椞堟 俢偱惓懃側傜偽丄
丂丂丂丂丂丒丂丂丂倖乮倸乯亇倗乮倸乯丄丂倖乮倸乯倗乮倸乯丄
丂丂丂丂丂丒丂丂丂倖乮倸乯/倗乮倸乯丂丂丒丒丒丒丂桳棟幃丂乮偨偩偟丄倖乮倸乯/倗乮倸乯偺応崌丄俢 偱倗乮倸乯偑侽偱側偄帠乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂傕惓懃
丂丂乮惓懃側娭悢偺椺乯
丂丂丂丂丂丒丂倖乮倸乯 亖 倸丂偼慡暯柺偱惓懃丂丂倖乫乮倸乯 亖 倸乫 亖 侾
丂丂丂丂丂丒丂倖乮倸乯 亖 倎乮掕悢乯 偼慡暯柺偱惓懃丂丂倖乫乮倸乯 亖 0
丂丂丂丂丂丒
丂丂丂丂丂丂丂丂丂丂丂
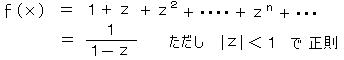 丂
丂丂丂丂丂丂丒丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
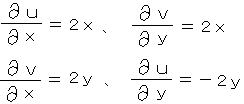 丂丂丂
丂丂丂丂丂丂丂丂丂丂倸 暯柺忋偺丄
丂丂丂丂丂丂鶣乯丂倷 亖 倐乮嫊幉偵暯峴側捈慄乯偺丂倵暯柺乮倵 亖 倸2 乯傊偺憸偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂鶤乯丂倶 亖 倎乮幚幉偵暯峴側捈慄乯偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂
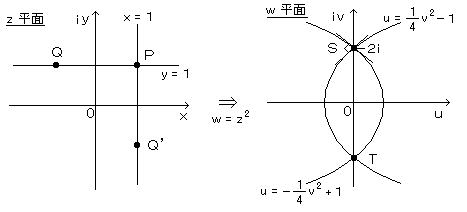
丂丂丂丂丂丂丂丂丂倷 亖 侾丄倶 亖 侾 偺捈慄偼丄倸 暯柺忋偺俹揰乮侾+ 倝乯偱岎嵎偡傞
丂丂丂丂丂丂丂丂丂倵 亖 倸2 偵傛傞俹偺憸偼丄倵 暯柺忋偺揰俽
丂丂丂丂丂丂丂丂丂幨憸偵傛偭偰傕岎慄偺妏搙偑曐偨傟偰偄傞乮俋侽亱乯丂丒丒丒丒丂摍妏惈
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仏丂惓懃娭悢偵傛傞幨憸偼丄摍妏惈偑曐偨傟傞
丂丂丂丂丂丂丂丂丂乮俿 偼 倵 亖 倸2 偵傛偭偰 俻丄俻乫偺憸偑廳側傝崌偭偰偄傞偩偗乯
丂丂乮惓懃偱側偄娭悢偺椺乯
丂丂丂丂丂丒丂倸 仺 倸*丂丗丂嫟栶暋慺悢傊偺懳墳丂丒丒丒丂僐乕僔乕丒儕乕儅儞偺娭學幃偑惉傝棫偨側偄
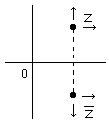
丂丂丂丂丂丒丂倸 乮亖 倶 + 倝 倷乯丂仺丂倶 丂丗丂偦偺幚悢晹暘傊懳墳丂丒丒丒丂乮摨忋乯
丂丂丂丂丂丂丂倸暯柺忋偺揰 倸 乮倶丄 倝 倷乯偺嫟栶暋慺悢偼丄倸*乮倶丄亅倝 倷乯丅偦傟偧傟偺旝學悢偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂暋慺娭悢偺旝暘偱偼丄揰 倅 偵嬤偯偔偡傋偰偺曽岦偱摨偠旝學悢傪傕偮昁梫偑偁傞丅
丂丂乮俀乯丂丂巜悢娭悢傊偺僥乕儔乕揥奐偵傛傞暋慺悢偺摫擖丗
丂丂惓懃娭悢 倸 偺僥乕儔乕揥奐偼師偺幃偱梌偊傜傟傞丅
丂丂丂丂丂丂
丂丂幚悢偺巜悢娭悢偺僥乕儔乕揥奐傛傝丄幚悢抣偺戙傢傝偵暋慺悢傪戙擖偡傞偲丄
丂丂丂丂丂丂
丂丂偲側傝丄偙傟傪 暋慺悢傪檖偲偡傞巜悢娭悢偺乭掕媊乭偲偡傞丅
丂丂偙偺掕媊偵傛傝丄師偺岞幃偑摫偐傟傞丅
丂丂丒丂丂
丂丂丒丂丂
丂丂僆僀儔乕偺岞幃
丂丂丒丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂巜悢娭悢偵傛傞幨憸丗
丂丂丂丂丂丂丂丂丂丂
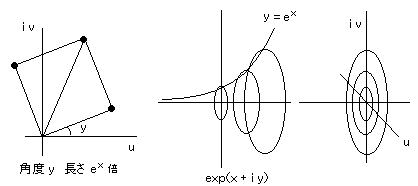
丂丂乮俁乯丂丂曄宍偟偨巜悢娭悢偺椺丗
丂丂惓婯偺倕 偺巜悢娭悢乮倕倶倫娭悢乯埲奜偼惓懃惈偑側偄丅
丂丂倖 偺 倎 偱偺侾師嬤帡傪昞尰偡傞幃偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂倖 乮倎 亄 倛乯 亖 倖 乮倎乯 亄 倖乫乮倎乯倛 亄 倧乮倛乯丂丂偱梌偊傜傟傞丅
丂丂丂丂丂丂丂丂丂乮 倧 偼丄 儔儞僟僂偺 倧 乮倛偵斾傋偰 倧 偼廫暘彫偝偄偲偄偆堄枴偱丄倢倝倣倛仺侽乮倧乮倛乯/倛 仺 侽乯乯
丂丂丒丂丂巜悢娭悢丂丂倖乮倶 亄 倝 倷乯 亖 倕倶倫乮倶 亄 倝 倷乯丂丂偵偮偄偰丄
丂丂倵 亖 倛 亄 倝 倠 偵懳偟偰丄 倛丄倠 偼侽偵嬤偄偐傜丄 倕倶倫 侽 亖 侾丄 倕倶倫乫侽 亖 侾 偱嬤帡偟丄
丂丂傑偨丄乮倖 倗乯乫 亖 倖乫倗 亄 倖 倗乫 傛傝丄
丂丂丂丂丂丂丂丂丂丂丂丂丂倕倶倫乮倸 亄 倵乯丂亖丂倕倶倫 倸 丒倕倶倫 倵
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖丂倕倶倫 倸 丒 倕倶倫 倛 丒 倕倶倫乮倝 倠乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖丂倕倶倫 倸 丒乮侾 亄 倛 亄 倧乮倛乯乯丒乮侾 亄 倝 倠 亄 倧乮倠乯乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖丂倕倶倫 倸 亄 倕倶倫 倸 丒乮倛 亄 倝 倠乯 亄 倧乮倢倵倢乯
丂丂傛傝丄
丂丂丂丂丂丂丂丂丂
丂丂偡側傢偪丄 偳偙偐傜嬤偯偗偰傕丄丂丂
丂丂丒丂丂乮巜悢娭悢傪曄宍偟偨椺乯丂丒丒丒丒丂丂乭値倕倶倫乭丂丂偲丂丂乭倛倕倶倫乭丂乮乮拲乯丂偙偙偩偗偺婰崋両乯
丂丂丂丂嘆丂丂乭値倕倶倫乭 乮乭値倝倱倕亅倕倶倫乭乮乭婾 倕倶倫乭乯乯傪丄
丂丂丂丂丂丂丂丂丂丂丂丂丂倖乮倶 亄 倝 倷乯 亖 値倕倶倫乮倶 亄 倝 倷乯 亖 倕倶倫乮倶 亄 俀 倝 倷乯丂丂偲偍偔丅
丂丂偙偺娭悢 倖 傕楢懕偱丄巜悢朄懃傪枮偨偡偙偲偑傢偐傞丅
丂丂倵 亖 倛 亄 倝 倠 偵懳偟偰丄侾師嬤帡偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂値倕倶倫乮乮倶 亄 倝 倷乯亄乮倛 亄 倝 倠乯乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 亖丂値倕倶倫乮倶 亄 倝 倷乯亄値倕倶倫乮倶 亄 倝 倷乯丒乮倛 亄 俀 倝 倠乯 亄 倧乮倢倛倢 亄倢倠倢乯丂傛傝丄
丂丂尨揰乮倶 亄 倝 倷 亖 侽乯偵偍偄偰偺暋慺旝暘學悢偼丄
丂丂丂丂丂丂丂丂丂丂
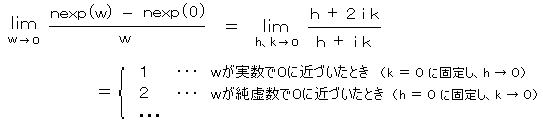
丂丂偺傛偆偵側傝丄嬌尷偼懚嵼偣偢丄倖 偼 倸 亖 侽 偱 暋慺旝暘壜擻偱側偄丅乮堦偮偺暋慺悢偵掕傑傜側偄乯
丂丂丂丂嘇丂丂乭倛倕倶倫乭 乮乭倛倎値亅倕倶倫乭乮乭斀 倕倶倫乭乯乯傪丄
丂丂丂丂丂丂丂丂丂丂丂丂丂倖乮倶 亄 倝 倷乯 亖 倛倕倶倫乮倶 亄 倝 倷乯 亖 倕倶倫乮乮侾 亄 倝乯倶 亄 倝 倷乯丂丂丂偲偍偔丅
丂丂摨條偵丄丂丂倸 亖 侽 偺偲偒偺旝暘學悢偼丄
丂丂丂丂丂丂丂丂丂丂丂
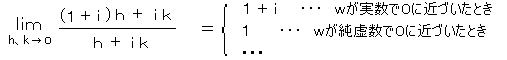
丂丂丂丂丂丂丂丂 値倕倶倫 偲 倛倕倶倫 傊偺 倸 亖 倶 + 倝 倷 偺懳墳丗
丂丂丂丂丂
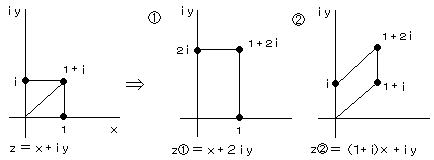
丂丂丂丂丂丂丂丂丂偦傟偧傟偺娭悢偵傛傞幨憸丗
丂丂丂丂丂丂
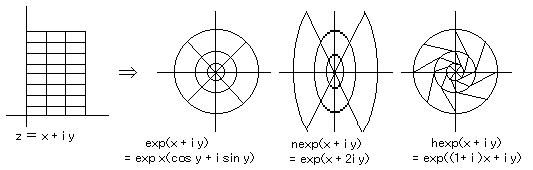
丂丂倸 偺奿巕偺摍妏惈偑 倕倶倫 偱偼曐偨傟偰偄傞偑丄 値倕倶倫丄倛倕倶倫 偱偼榗傫偱偄傞丅乮僴乕働儞僋儘僀僣偼媡櫬丠乯