４． 無限級数形式の美 ＋ オイラーの定数
４−2 級数の中の虚数の振舞い（証明・導き方）
無限級数形式の記述は、指数関数に複素数が導入される方法として用いられたように、虚数単位 ｉ の性質が効果的に用いられる不思議な摂理になっている。無限級数のダイナミックな演算において、特に、虚数単位の振る舞いは、数式の証明に用いられるほどの単純明快さを持った美しさがある。（聖霊様による証しを思わせる！）
そして、オイラーの公式の π、ｅ、ｉ の絶妙な関係が常に用いられているのを見ることができるのである。
また、調和級数の総和と自然対数との差によって定義されるオイラーの定数 γ やゼータ関数（ζ 関数）は、素数という数論上の直線的で孤独な数に密接に関連している。
（１） 無限級数の比較： 比較のために級数を列挙する。
・ 自然対数の底： 自然対数の底 ｅ そのものは、純粋に解析的に定義された数であり、虚数単位を用いずに導かれる。
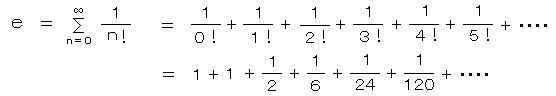・・・１）ｅ は、ｅ ＝ ２．７１８２８１８２８４５９０４５・・・・・に収束する。
分母の階乗は、指数関数が微分しても変わらないこと、ｅｘｐ 0 ＝ １、および、整式の係数が微分毎に次数が下がって出ること、によって現れる。 ・・・・ ｅ は”解析的な数” （ｃｆ． ｉ は”代数的な数”、ｅｘｐ ｘ が級数の形になって初めて導入できる。ちなみに πは”幾何的数”。）
・ 調和級数 Ｓ1 と Ｓ2、Ｓ4、・・・など：
（ｐ は正の整数） とすると、
・・・ 調和級数 ２）発散の証明は古くから成されていた。
発散の速度は非常に小さい
（オイラー 1735） ３）＝ １．６４４９３４０６６８・・・・・・
・・・ ４）＝ １．０８２３２３２３７１１・・・・・
ｐ が偶数のときはオイラーが公式を発見した。
しかし、奇数の時はよくわかっていない（ベルヌーイ数を用いたラマヌジャンの複雑な表示式はある）
・ いくつかの類似した無限級数：
・・・ ６）ｌｎ（１＋ｘ）の無限級数に ｘ ＝ １を代入
・・・ グレゴリーの式 ７）πの計算には収束が遅い
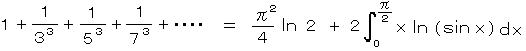８）Ｓ3 まではいかなかった（Ｓ3、Ｓ5以降 はよく知られていない）
・・・・ ９）（ｘ の ｘ 乗） ＝ ｅｘｐ（ｘ ｌｎ ｘ） を使用
級数に展開した状態で、π、ｅ （あるいは ｌｎ）、ｉ が、主としてオイラーの公式を出発点として、自由に用いられ、各項ごとの演算を行うことができる。
⇒ 証明・導き方
（２） オイラーの定数 γ：
γは、調和級数 Ｓ1 の ｎ 項までの部分和 Ｓ1(n) から ｎ の対数を引いたもので、
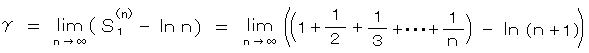
＝ ０．５７７２１５６６４９０１５３２８・・・・・（収束） ・・・ ５）
これは調和級数による有理数的な凹凸を、なめらかな自然対数で吸収した差分を表し、
無限大の極限では両者は一致する。これは、連続関数ならば分数関数を積分すると
対数関数になる事を思わせるが、未だγが有理数か無理数かさえも知られていない。
・ Ｓｐ の残りの数値（ｐ＝３以上の奇数）が未知でも、γとの関係式が与えられている。
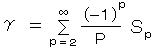・・・・・ １０）・ ゼータ関数を、Ｓｐの ｐ を複素数まで拡張し、次のように定義する。
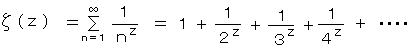・・・ ｚ 実数部を含む複素数ｐ が素数の場合の驚くべき関係式が導かれる。ゼータ関数は、素数の分布に関連した関数である。
ｚ の実数部が１より大きい場合収束する。
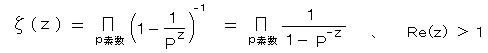・・・ オイラー積・・・・ １１）
また、オイラーは、
・・・・・ １２）を証明したが、これは素数が無限に存在することよりも強いものである。この式は、Ｓ1よりもさらにゆっくりと発散する。