４－2 級数の中の虚数の振舞い ・・・ ４．の無限級数の証明
・ ２）式 調和級数の総和が発散する事：
古典的でエレガントな証明である。
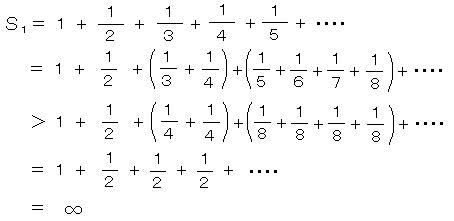
（ﾆｺﾙ･ｵﾚｽﾑ 1350？・仏）
マイナスや虚数の概念はこの時代には無かった。学者の間でも、マイナスは不吉なものとしてタブー視されていた。この時代の十字架信仰がなっていないことと同じである！。 調和級数の和の発散はおそろしく遅く、１００億項目までの部分和が約２３．６。 Ｓ1の部分和が１００に達するには、１．５×１０の４３乗以上の項が必要。 それでも ∞ に発散する！。
・ ３）式 Ｓ2 ＝ π2/６：
三角関数のべき級数展開
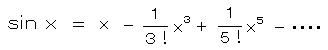より、次の無限次多項方程式
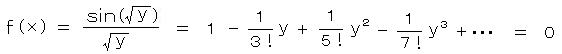・・・ ①をつくる。
これは、ｓｉｎ（√ｙ） ＝ ０ の時にのみ根が存在する。 上式の右辺は ｙ ＝ ０ のとき １になるから ｙ ＝ ０ は根ではない。すなわち、根は、
（ｎ は０でない任意の整数） あるいは、
・・・ ②
ここで、多項方程式
には代数学の基本定理より ｎ 個の根 ｒｉ が存在し、左辺は因数分解されて
ｘ の（ｎ－１）乗の係数は
となることより、
について、
これが無限次の多項方程式にも成り立つとすると、 ａ1 すなわち ①の級数の２項目は、②を用いて、
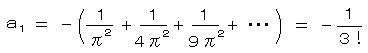
したがって、 Ｓ2 ＝ π2/６ を得る。 （ｵｲﾗｰ・1739）
・ ６）式 メルカトルの式：
幾何級数の式（＊ 級数に公比をかけて引くと得られる）
を積分すると、
出てくる積分の不定定数は、ｚ ＝ ０ とおけば 両辺が０となって消去される。 （ﾆｺﾗｽ･ﾒﾙｶﾄﾙ 1668・ﾃﾞﾝﾏｰｸ）
また、ｚ ＝ １ とおけば
となる。
・ ７）式 グレゴリーの式の証明：
虚数単位の性質を利用して、π の値を計算する式を導く。（ ｉ からπが出てくる！）
オイラーの関係式から、ｅｘｐ（ ｉ π/２ ） ＝ ｉ より、さらに ｉ そのものが自在に変化して、
メルカトルの式から、 ｚ ＝ ｉ として 対数を展開すると、
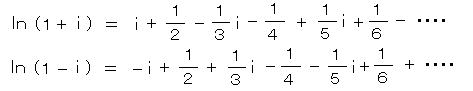
両式の各項どうしを引いて
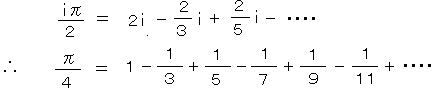
（ｼﾞｪｰﾑｽﾞ･ｸﾞﾚｺﾞﾘｰ 1671・ｽｺｯﾄﾗﾝﾄﾞ）
グレゴリーの式は、πを計算するには収束が非常に遅く全く実用的でない。そのため改良が考えられ、いくつかの式（シェルバッハ、マシン）が同様にして導かれた。
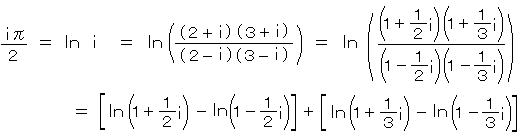
対数を展開して
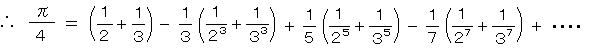
また、さらに収束を速めて、
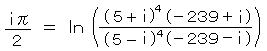より、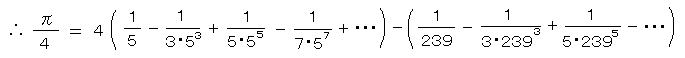
＝ ４ ｔａｎ‐1（１/５） － ｔａｎ‐1（１/２３９） （シェルバッハ/マシンの式・1706）
この式を用いて、約２５０年後（1949）に世界最初の電子計算機 ＥＮＩＡＣ が πを２０００小数位以上計算した。現在でも収束の早い式として知られている。
・ １０）式 Ｓｐ と γ の関係式：
メルカトルの式
に ｚ ＝ １、１/２、１/３、１/４、・・・ を代入すると、
これらの式を加え合わせると、対数の項は ｌｎ （ｎ＋１） のみが残り、
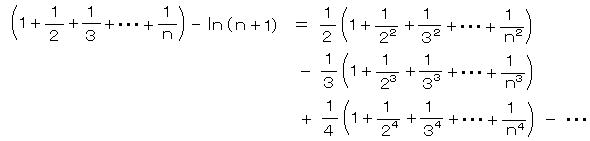
したがって、オイラーの定数 γ と ｐ が２以上の Ｓｐ との関係式が導かれる。
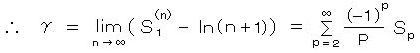
・ １１）式 オイラー積：
ゼータ関数による素数の分布の表示式を計算する。
ζ（ｚ）に１/２＾ｚをかけると、
これをζ（ｚ）から引くと、
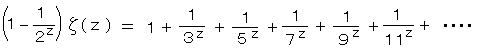
これに１/３＾ｚをかけると、
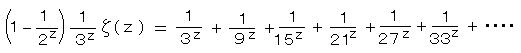
これを（１－１/２＾ｚ）ζ（ｚ）から引くと、
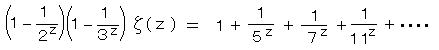
このように、１/ｎ＾ｚ（ｎ ＝ 素数）を逐次かけて上の式から引く操作を繰り返すと、素数の倍数をすべて引き去ることになり、オイラー積
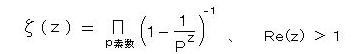
が導かれる。
・ １２）式 素数の無限性：
オイラー積の式で、 ｚ ＝ １とおくと、
両辺の対数をとると、総積の対数は総和になるから、
メルカトルの式に ｚ ＝ －１/Ｐ とおいて対数部分を展開すると、
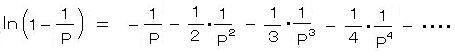
より
右辺の第２項は幾何級数とみなすと、
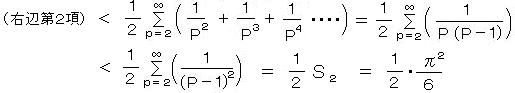
したがって、
Ｓ1 ＝ ∞ より、 ｌｎ （Ｓ1） ＝ ∞ 、 ゆえに、
