丂丂丂丂丂丂丂丂俆亅俁丂丂僐乕僔乕偺愊暘掕棟丗
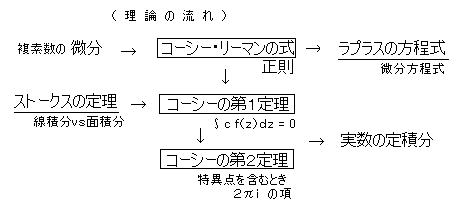
丂丂楌巎揑側敪尒弴偲偼媡偱偁傞偑丄僗僩乕僋僗偺掕棟傪愭偵弎傋偰崪慻傒傪嶌傝丄偦傟偐傜 僐乕僔乕偺愊暘掕棟乮1814乯偵峴偭偨曽偑棟夝偑偟傗偡偄偲巚傢傟傞丅
丂乮僗僩乕僋僗偺掕棟偼丄僌儕乕儞偺掕棟丄僈僂僗偺掕棟丄儘僔傾偱偼僆僗僩儘僌儔僘僉乕偺掕棟偲傕屇偽傟傞丅侾俋悽婭偺帪戙偼丄揹帴婥傗棳懱丄廳椡偺棟榑偱丄懱愊偲嬋柺偺愊暘偺栤戣偱昁梫偲偝傟偰偄偨偺偱丄摨帪偵懡偔偺恖偑曬崘偟偨丅乯
丂丂愊暘寁嶼偵梡偄傜傟傞僐乕僔乕偺
戞侾愊暘掕棟偼丄暋慺暯柺偵偍偗傞娭悢偺惂尷帠崁偱偁傞惓懃惈丄偍傛傃丄嵟傕捈姶揑偵暔棟揑側奣擮偺幃傪摫擖偱偒傞 儔僾儔僗偺幃乮挷榓曽掱幃乯偲摨偠偙偲傪尵偭偰偄傞丅
丂丂庡偑掕傔偨惓懃惈偲偄偆棩朄偼丄屼巕偺廫帤壦乮倕 丄兾乯偵傛偭偰姰慡偵惉廇偟丄惞楈條乮 倝 乯偵傛偭偰寢壥揑偵庣傞偙偲偑偱偒傞丅惓懃偱側偄摿堎揰傪娷傓応崌偱傕乮恀惈摿堎揰偱側偄偐偓傝乯敪嶶偺婋尟傪嗦嘞偵夞旔偡傞偙偲偑偱偒傞丅偡側傢偪丄摿堎揰偺傑傢傝傪堦廃偟偨師偺悽傊偺暅妶偵婓朷偑偐偗傜傟偰偄傞丅乮儘儅丂丂乯丂丂偙偺偲偒 検巕榑揑偵偼 検巕悢偑堦偮憹偊丄僄僱儖僊乕弨埵偑堦抜奒忋偑傞丅杤変偡傞傢偗偱偼側偄丅 偦偟偰暅妶乮堦廃 俀兾倝 乯偺偨傔偵偼丄屼巕偺廫帤壦偺帪乮兾倝 乯傪宱側偗傟偽側傜側偐偭偨両丅
丂丂乮侾乯丂丂僗僩乕僋僗偺掕棟丗
丂丂幚悢忋偺慄愊暘偲柺愊暘傪寢傃偮偗傞幃丅
丂丂幚暯柺撪偺愊暘楬 俠 傪嫬奅偲偡傞擇師尦揑曄堟 俼 偵偮偄偰丄
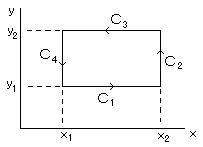
丂丂丂丂丂丂丂
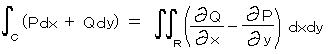
丂丂偨偩偟 俹丄俻丂偼 倶 偲 倷 偺幚娭悢丅
丂丂傑偢丄塃恾偺巐妏偄椞堟偵偍偗傞愊暘傪峫偊傞丅
丂丂塃曈偺戞擇崁偵偮偄偰丄
丂丂
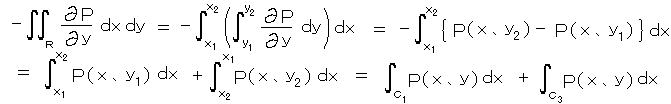
丂丂俠2 丄俠4 偵増偆応崌偼丄 倓倶 亖 侽 傛傝 偦傟傜偺愊暘偼 侽 偱偁傞偑丄偦傟傜傕宍幃揑偵偁傜傢偡偲丄
丂丂
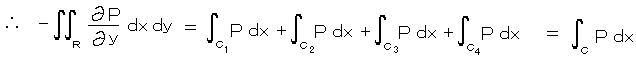
丂丂戞堦崁偵偮偄偰傕摨條偵丄俠1丄俠3 偵増偭偰 倓倷 亖 侽丂傛傝丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂師偵丄擟堄偺宍偺椞堟偵偮偄偰丄恾偺傛偆偵丄巐妏傪敄偄挿曽宍偵偟偰愊傒廳偹傞偲丄挿曽宍偳偍偟偑愙偡傞晹暘偼懪偪徚偟崌偄丄奜廃晹 俠 偺傒偑愊暘偵桳岠側峴掱偲偟偰巆傞丅
丂丂丂丂
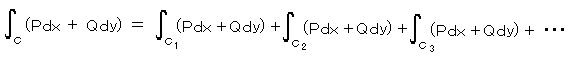
丂丂乮俀乯丂丂僐乕僔乕偺戞侾掕棟乮僐乕僔乕偺愊暘掕棟乯丗
丂丂暋慺暯柺忋偺宱楬愊暘傪峫偊傞丅
丂丂暋慺愊暘偺掕媊偼丄暋慺暯柺偺椞堟 俢乮俢 撪偵 宱楬 俠乯偱掕媊偝傟偨 楢懕娭悢 倵 亖 倖乮倸乯偵偮偄偰丄
丂丂丂丂丂丂
丂丂偨偩偟丄兲倝 偼 俠 忋偱 倸倝 偲 倸倝亄1 偺娫偵偁傞擟堄偺揰丅丂掕媊偺宍幃偼幚悢偺応崌偲摨偠偱偁傞偑丄僌儔僼偺偮偔傞柺愊偱偼側偔丄娭悢 倖乮倸乯 偺暯嬒揑嫇摦乮儀僋僩儖偺憤榓偺嬌尷乯傪堄枴偡傞丅
丂丂倖乮倸乯 傪 椞堟 俢 偱掕媊偝傟偨惓懃娭悢丄俠 傪 俢 撪偵偁傞扨堦暵嬋慄乮撪晹偲奜晹偑掕媊偝傟丄慄偼岎嵆偟側偄乯偲偡傞偲丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂偙傟偼丄惍幃乮懡崁幃乯傗廂懇墌撪偱偺傋偒媺悢偼丄巒揰 兛 偲廔揰 兝 偩偗偱抣偑寛傑傝丄倖乮倸乯 亖 俥乫乮倸乯 傛傝 俥乮倸乯偑惓懃娭悢偱偁傝丄佺俠 倖乮倸乯倓倸 亖 俥乮兝乯亅俥乮兛乯 偲側傝丄廂懇墌撪偵偁傞暵嬋慄偱偼 侽 偵側傞偙偲傪昞偟偰偄傞丅丂椞堟 俢 偵寠偑偁偄偰偄傞応崌丄偦偙偼乭奜晹乭偵側傞丅
丂丂倳 丄倴 傪 倶 丄倷 偺幚娭悢偲偟偰丄
丂丂丂丂丂丂丂丂
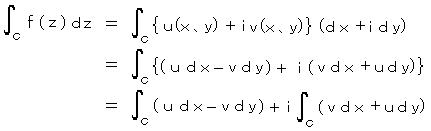
丂丂偙偙偱 僗僩乕僋僗偺掕棟傛傝丂俹 亖 倳丄 俻 亖亅 倴 偲偍偔偲丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
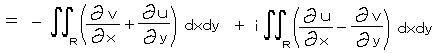
丂丂
丂丂偦傟偧傟偺愊暘撪偼丄倖 偑惓懃娭悢偱偁傞忦審偐傜丄倳丄倴 偼 僐乕僔乕丒儕乕儅儞偺曽掱幃
丂丂丂丂丂丂丂丂丂丂
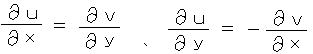 丂丂傪枮偨偡偺偱丄
丂丂傪枮偨偡偺偱丄丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亪丂
丂丂偙偺晄巚媍側掕棟偼 幚悢懱偵偼尒傜傟側偐偭偨傕偺偱丄偙偺傛偆偵乭惓懃惈乭偺忦審偐傜棃偰偄傞丅 偳傫側娭悢偱偁偭偰傕丄偨偩 乭惓懃乭 偱偁傞偲偄偆偙偲偩偗偱丄暋慺暯柺忋傪堦廃偟偰愊暘偡傞偲 侽 偵側傞偺偱偁傞両 乮媡乮愊暘偑侽偱偁傞側傜 倖 偼惓懃乯傕傑偨恀偱偁傞偙偲傕 屻偺帪戙偵徹柧偝傟偨乯
丂丂惓懃惈偼丄惍幃丄乮暘曣偑 0 偱側偄乯桳棟幃丄偦偟偰 巜悢娭悢乮亄 嶰妏娭悢乯丄偍傛傃 偦傟傜偺慻傒崌傢偣偺傒偑僋儕儎乕偡傞丅
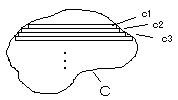
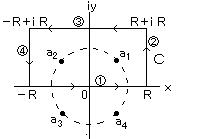
丂丂乮俁乯丂丂僐乕僔乕偺戞俀掕棟乮僐乕僔乕偺愊暘岞幃乯丗
丂丂偱偼丄愊暘楬偺拞偵 娭悢偑乭惓懃偱側偄乮夝愅揑偱側偄乯揰乭 傪娷傓応崌偼偳偆側傞偩傠偆偐丠
丂丂偨偲偊偽丄暘悢幃丂倖乮倸乯/乮倸 亅 倸0乯丂偼 倸 亖 倸0 偱 敋敪乮亣 偵敪嶶乯偡傞両 偦偺傛偆側揰偼丄侾埵偺摿堎揰乮偁傞偄偼 扨弮側嬌乯偲屇偽傟偰偄傞丅 倖乮倸乯/乮倸亅倸0乯2丄倖乮倸乯/乮倸亅倸0乯3丄偼 俀埵丄俁埵偺摿堎揰傪傕偮偲偄偆丅 暘悢幃偺愊暘偼摿堎揰傪摿暿側曽朄偵傛偭偰張棟偟側偗傟偽側傜側偄丅
丂丂榑棟揑揥奐偲偟偰偼丄摿堎揰傪乭奜晹乭偺揰偲偟偰旔偗 偦偺椞堟偱娭悢偑惓懃偱偁傞偲偟
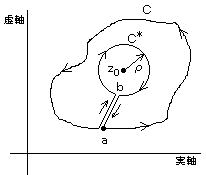 偰 戞侾掕棟傪揔梡偟丄偦傟偐傜嬌尷傊傕偭偰偄偔丅
偰 戞侾掕棟傪揔梡偟丄偦傟偐傜嬌尷傊傕偭偰偄偔丅丂丂恾偺傛偆偵丄 倎 偐傜弌敪偟偰 俠 - 倎倐 - 俠 * - 倐倎 傪捠偭偰 倎 偵栠傞宱楬傪峫偊傞丅 俠 * 偼 倸0傪拞怱偲偡傞 敿宎 兿 偺墌偲偡傞丅 偙偺宱楬偼丄乭扨堦暵嬋慄乭偵側偭偰偄偰丄摿堎揰 倸0 偼嬋慄偺乭奜晹乭偵偁傞丅
丂丂偟偨偑偭偰丄偙偺暵嬋慄撪偱偼 倖乮倸乯/乮倸 亅 倸0乯 偼惓懃側偺偱丄
丂丂僐乕僔乕偺戞侾掕棟傛傝丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
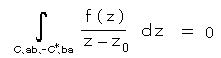 丂
丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
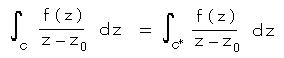
丂丂俠*偼 倸0傪拞怱偲偡傞墌偩偐傜丄丂俠* 忋偱丂丂倸 亖 倸0 + 兿倕倶倫乮倝兤乯丂丄 倓 倸 亖 倝 兿倕倶倫乮倝兤乯倓兤丂偲偍偗傞偺偱丄
丂丂
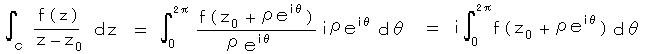
丂丂偙偙偱丄乥倕倶倫乮倝兤乯乥偼 兿 偵傛傜偢桳尷側偺偱丄 兿 仺丂0丂偵偡傞偲丄 倖乮倸0亄兿倕倶倫乮倝兤乯乯 偼 掕悢 倖乮倸0乯 偲側偭偰愊暘偺奜偵弌偣傞偺偱丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂偟偨偑偭偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
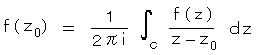 丂丂丂丂丂乮僐乕僔乕偺戞俀掕棟乯
丂丂丂丂丂乮僐乕僔乕偺戞俀掕棟乯丂丂乮係乯丂丂棷悢乮傝傘偆偡偆乯丗
丂丂幚悢偺掕愊暘偺拞偵偼丄棷悢傪梡偄偰斾妑揑梕堈偵夝偗傞応崌偑懡偄丅
丂丂棷悢傪丄摿堎揰乮屒棫摿堎揰乯 倎 偲偟偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂
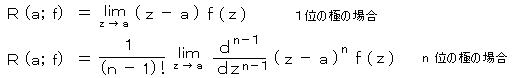
丂丂偲掕媊偡傞丅丂偡傞偲丄丂僐乕僔乕偺戞俀掕棟偼 棷悢偵傛偭偰奼挘偝傟丄
丂丂丂丂丂丂
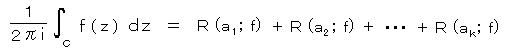
丂丂偙偺 倎侾偐傜 倎倠 傑偱偼 俠 偺撪晹偵偁傝丄 奜晹偺揰偺棷悢偼 戞侾掕棟偵傛傝 偡傋偰 侽 偲側傞丅
丂丂丒丂椺乯
丂丂丂丂丂丂丂丂
丂丂丂
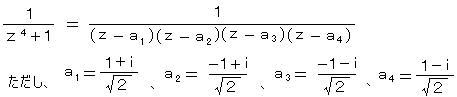
丂丂偲側傝丄 倎侾 乣 倎係丂偼 偦傟偧傟 倖乮倸乯 偺 侾埵偺嬌偵側偭偰偄傞丅
丂丂恾偺傛偆偵愊暘宱楬傪偲傞偲丄俠 偺撪晹偵偁傞偺偼 倎1丄倎2 偺傒偱丄
倎3丄倎4 偼彍奜偝傟傞丅
丂丂棷悢傪寁嶼偡傞偲丄
丂
丂丂摨條偵丄丂丂
丂丂備偊偵丂丂
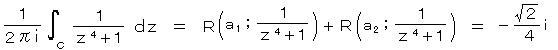
丂丂宱楬 俠 傪 恾偺嘆偐傜嘋傑偱偵暘偗傞偲丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂嘆 偼 幚幉忋偺愊暘偵側傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂嘇嘊嘋 偼 師偺寁嶼偱偡傋偰 侽 偵側傞丅
丂丂
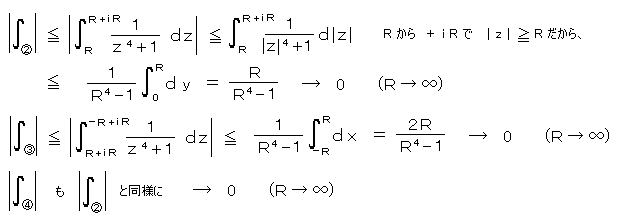
丂丂偟偨偑偭偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
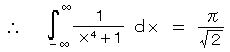 丂丂傪摼傞丅
丂丂傪摼傞丅丂丂乮俆乯丂丂儘乕儔儞揥奐偲恀惈摿堎揰丗
丂丂僥乕儔乕揥奐傪丄晧傋偒偺崁傑偱奼挘偟偨傕偺傪丄儘乕儔儞揥奐偲偄偆丅僐乕僔乕偺戞俀掕棟偐傜 倎 傪拞怱偲偡傞 奜懁偺墌 俠 偲 撪懁偺墌 俠 * 偵増偭偰丄
丂丂丂
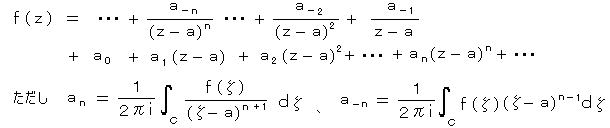
丂丂偑摫偐傟傞丅 乮乮俠 偺愊暘乯 亖 亅乮俠 * 偺愊暘乯乯丂摿偵丄倎-1 偼 棷悢丂丂
丂丂儘乕儔儞揥奐偼丄摿堎揰 倎 偺敾暿偵梡偄傜傟傞丅
丂丂丂鶣乯丂彍嫀壜擻側摿堎揰丗丂倢倝倣倸仺倎 倖乮倸乯 亖 俙丂丂乮俙丗桳尷側暋慺悢乯丂丒丒丒丂晧傋偒崁傪娷傑側偄
丂丂丂鶤乯丂倣埵偺嬌偲側傞摿堎揰丗丂倢倝倣倸仺倎 倖乮倸乯乮倸 亅 倎乯 亖 俙丂丂乮値亖倣乯丄丂亖 亣丂乮値亙倣乯丂丒丒丒丂晧傋偒崁偼桳尷屄
丂丂丂鶥乯丂恀惈摿堎揰丗丂倢倝倣倸仺倎 倖乮倸乯乮倸 亅 倎乯丱値 亖 亣丂丂乮偡傋偰偺 値 偵偮偄偰乯丂丒丒丒丂晧傋偒崁偼柍尷屄
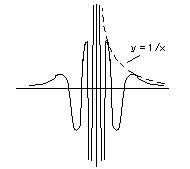
丂丂倕倶乯丂恀惈摿堎揰偺椺丟
丂丂丒丂丂
丂丂丂丂丂
丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮乽偨偩丄柵傃偺巕偑柵傃傑偟偨丅乿乯