　　　　　　　　５．　複素数の積分の思索

　　　　　　　　　　　　　　　　　　　　　　　　　　５－２　複素積分の実例　　　　５－３　コーシーの積分定理

　歴史的に見て、 π、ｉ、ｅ は、それぞれ、空間、量、変化の思索に対応する、初等的なそれぞれ幾何、代数、解析から現われ、別々に定義された。そしてこれらの”３者”は、オイラーの公式において”一体”となって、さらに多くの発展的な分野に成長していった。（＊）
　実数の定積分の中には、複素数まで数の領域を拡張して初めて算出されるものが多く存在するのは驚くべきことである。しかも、それらの結果は、物理や工学などの、実りある、現実的な自然現象についての思索分野へと流れし出している。その導出の過程において、発想を切り替え、それぞれ視覚的な思索（π）、数式のパターン認識の思索（ｉ）、極限の思索（ｅ）が充分に用いられている。

　（＊　代数、幾何、解析。初等数学の多くの分野は一つの式に合流し、そしてそれを起点に再び奔流となって流れ出る。音楽芸術で言えば、それまでの様式が全部流れ込み、そこから再び出ていった、Ｊ．Ｓ．バッハのような存在である。　自然対数の底、円周率、虚数単位、指数関数、三角関数が織りなす不思議なオイラーの公式が奏でる優美なハーモニー。ニュートン力学でさえもそれまでの幾何学形式で書かれていたので、オイラーが定式化して公表したと言われる。
　ユダヤ人物理学者のファインマンは、オイラーの公式のことを、「これは我々の至宝である」と嘆じた。　オイラーもバッハも敬虔な異邦人クリスチャンであり、また同時に非常な多作家であった。　→　バッハについて　）

　　（１）　　ガウス積分：　　・・・　ガンマ関数に見る思索の用いられ方

　　まず、実数のみで、上の３つの思索パターンを見る。
　　ガンマ関数を、
　　　　　　　　　　　　　　　　　と定義すると、
　　積分の内部は指数関数と整式の積の形になっていて、ｎ＞１ならばｘ→∞で ∞/∞の形になっている。
　　明らかに、　　　　　　　　　　　Γ（１）＝１
　　部分積分より、　　　　　　　　Γ（ｎ + １）＝ｎ Γ（ｎ）　となるので、　　　　・・・・　　１）
　　ｎ＝１、２、・・・、ｎを　逐次代入すると、
　　　　　　　　　　　　　　　　　　　Γ（ｎ）＝（ｎ－１）！

　　ここで、ｎを、負の数を含むすべての実数に拡張すると、たとえば、ｎ＝１/２について、

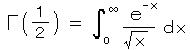　　　　　　　　　　　　　　　　　　を計算する。

　　　とおいて変数置換すると、　ｄｘ＝２ｔｄｔ　　より、
　　　　　　　　　　　　　　　　　　　ここで、さらにｕ、ｖを用いて
　　　　　　　　　　　　　・・・・　　２）　とおくと、平面的な重積分
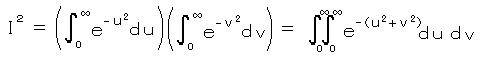　　　　　　　を作ることができる。
　　これは　ｕ、ｖ－平面の第一象現（０＜＝ｕ＜ ∞、０＜＝ｖ＜ ∞）に渡っての積分と見ることができる。
　　さらに、ｄｕｄｖ＝ｒｄｒｄθ、ｕ＝ｒｃｏｓθ、ｖ＝ｒｓｉｎθ によって 極座標に変換すると、ここで初めて 不定積分を計算することができて、
　　　　　　　　
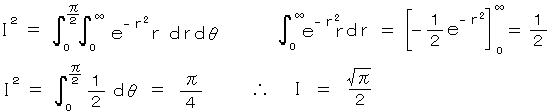
　　したがって、　　　　　を得る。　　　　　　　　　　　・・・・　　３）

　　１）３）によって、さらに　　　Γ（－１/２）＝１/（－１/２）・Γ（１/２）＝－２ Γ（１/２）＝－２√π、
　　　　　　　　　　　　　　　　　　Γ（３/２）＝１/２Γ（１/２）＝１/２・√π、　・・・

　　計算可能な不定積分に導くことが目的であるが、平面化、および、極座標への変換は”幾何の思索”（図形のパターン認識）により成され、この図形的な発想によって π が入ってきた。
　　また、上記の　２）を書きなおして３）より、

　　　　　　　　　　　　　　　　　　　　
　　これは ガウス積分 と呼ばれ、確率論に用いられる。
　　・・・・　　ガウス積分は導出過程でｉを使わないでできたので、ｉのない理論へ用いられた。→　統計学、統計力学（それゆえ砂の集合体を扱う、”死のｅ” ）

　　（２）　　フレネル積分：　　・・・　変数に複素数を導入

　　次に Γ 関数を複素数まで拡張する。 Γ関数に、　　（ｐ、ｑは正の実定数）を代入すると、
　　　　　　　　　　　　
　　これは、元の Γ（ｎ）の積分の道は実のｘ軸に沿っていたが、この変換された積分は実軸に対し α ＝ｔａｎ‐1（ｑ/ｐ）だけ傾いている。　　ダミー変数ｕをそのままｘに戻すと、
　　　　　　　　　　　　
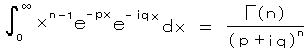
　　極形式に変換すると、　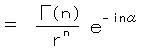　　　　　　　　　　　　　　　　　ただし、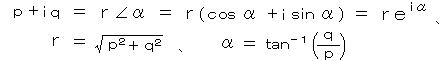
　　　　　　　　　　　　　　　　　　　

　　ここで オイラーの公式より、ｅｘｐ（－ｉｑｘ）とｅｘｐ（－ｉｎα）をｃｏｓ、ｓｉｎの形にして、実部と虚部に分ける（実・虚等値）と、
　　　　　　　　　
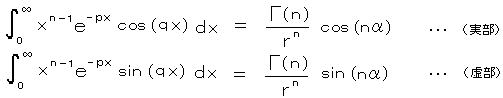
　　ｎ＝１/２、ｐ＝ 0、ｑ＝１とおくと、　α ＝ｔａｎ‐1（１/０）＝ｔａｎ‐1（∞）＝ π/２、ｒ＝１、 Γ（１/２）＝ √π より、
　　　　　　　　　　　　　　
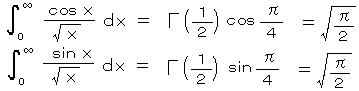
　　θ ＝ √ｘ　とおくと　ｄθ ＝２ｄｘより、
　　　　　　　　　　　　　・・・・　フレネル積分

　　（　・・・　三角関数が出てくるということは、オイラーの公式によりｉに関わってｅが変換され、光の振動・波動などの、”神の性質”に関わる理論が導かれてくる。（ただし、この時点の物理学では、虚数は媒介であって、実数という表面上の実だけを見ているのであるが））

　　（３）　　ディリクレの不連続積分：　・・・　極限と不連続の思索

　　　　　　について、同様に、オイラーの公式により実部、虚部に分け、
　　　　　　　　　　　　　　　
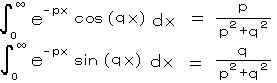
　　上の式（実部）のみについて、
　　ｐを固定して、ｑについてａからｂまでの積分を作ると、
　　　　

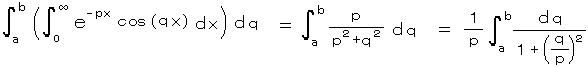
　　左辺の２重積分の順序を逆にして　（　注）被積分関数の連続性と収束の条件が必要（証明略））、
　

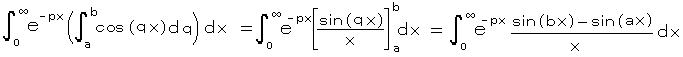
　　右辺について、　ｕ＝ｑ/ｐとおくと、ｄｕ＝（１/ｐ）ｄｑ　より、
　　　　　　　　　　　

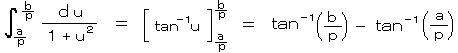
　　したがって、ｂ＝０　とおけば　右辺＝左辺は、
　　　　　　　　　　　
　　ｐ → ０　とすれば、
　　　　　　　　　

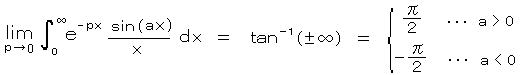
　　ここで、極限と積分の演算との順序を交換できると仮定すれば、（証明略）
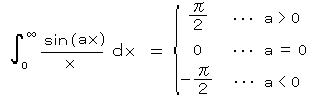
　　　　　　・・・・　ディリクレの不連続積分
　　　　　　　　特に、ａ＝１　のとき、　　　　　　

　　（４）　　オイラーの反射式：

　　Γ関数をによって変数変換すると、　
　　ｎを１－ｎで置きかえると、　　　　　　　　　　　
　　Γ（ｎ）＝（ｎ－１）！より、積は　　Γ（ｎ）・Γ（１－ｎ）＝（－ｎ！）（ｎ！）　　と書ける。

　　　　　　
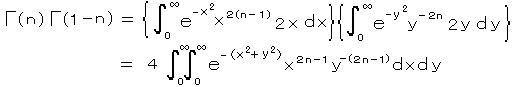
　　極座標に変換すると、　ｘ＝ｒｃｏｓ θ、ｙ＝ｒｓｉｎ θ、ｄｘｄｙ＝ｒｄｒｄθ、０＜＝ｒ＜＝ ∞、０＜＝ θ ＜＝ π/２　、　　となるので、
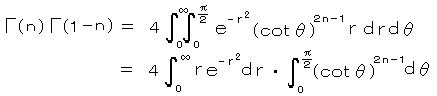　　　　　　　のように変数分離される。
　　　ｒについて、　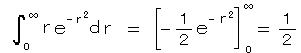　より、　
　　　ｃｏｔ θ ＝ｓ、　２ｎ＝ α　とおけば、
　　　　　　　　　　　　　　　　　　　　　　を得る。
　　　ド・モアブルの定理（＊）より　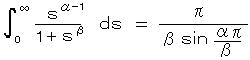　　であることが知られているので、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　・・・・・・　５－2（３）参照）
　　　β ＝２　に対し、　　　　　　　　・・・　オイラーの反射式（1771）

　　　（－ｎ）！ｎ！＝ｎπ/（ｓｉｎｎπ）　となり、　ｎ＝１/２　のとき　Γ（１/２）＝ √π　となる。