６． 本質的でない定数（黄金比、四元数単位）との比較
一般的に言われている数学定数の中には、単に伝統的なものや、従来のものに派生して創作されたものも含まれている。
古くからある”黄金比”は、視覚的に最も美しい（感性による評価）とみなされる数で、多くの美術的な理論付けに用いられてきたが、数学的には代数的無理数の一つに過ぎず、他の数学的基本数となって発展的に用いられるようなことはない。しかし黄金比は、自然の中にもいくつか見られるので、創造主の”感性”にかかわる不思議な数といえる。
複素数は、代数学のそれ自体で完結し、四則演算が自由にできる数の体系はこれ以外には存在しない事が明らかにされている。ちょっと考えてありそうな、”ｎ次元の数”は、 幾何学や極限（π 、ｅ ）の思索を用いないで、純粋に（初等）代数的手法のみによって否定される。
このような、創作的な（人工的な）思索の一つである、四元数（しげんすう）、八元数、十六元数などは、集合論的には興味深い題材であるが、実際的には 演算上の厳しい制限があり、自然の性質を表現するには不適格だと思われる。（四元数はグラフィックアートに用いられている。）
代数方程式の解として導入された虚数単位 ｉ が、もともと違う発想から始められた、異なる数学のカテゴリーである、解析学（微分）からの自然対数の底 ｅ と、初等幾何学からの円周率 π とに密接に関係し、エレガントな関係を持っていること自体が驚異である。思索の初めでは別々の「３者」が、途中で「一体」になって現れるのである！。
さらに、自然の本質である波動関数の世界が、複素数の範囲で構成されていることと調和している。古典物理では便宜上のものだったのが、量子力学では複素数は本質であり、全てである。
すなわち、神の性質の中心ポイントを表す、π、ｅ 、ｉ が、思索（数学）と現実（物理）の両方に共通して中心的に現れ、このことは、神が天地万物を造り、神に似せて人間を造った、という聖書の記事と非常によくマッチングしている。
（１） 黄金比の謎について：
黄金比は、ユークリッドの時代から発見され、線分を１：φ の比で分割した時や縦横の長さにした時、最も均斉が取れていると感じられる感性的な値で、
で与えられ、 
の解の一つであるので、φ＝１．６１８０３３９８・・・・ は代数的無理数に分類される。（ψ＝（－１＋√５）/２、ψ2＝１－ψとおいてもよい。この場合 ψ＝１/φ＝０．６１８０３３９８・・・となって、ψ：１＝ １：φ のように逆比になる）
これは、フィボナッチ数列
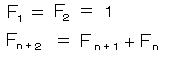
Ｆ ＝ １、１、２、３、５、８、１３、２１、３４、・・・・・・
の隣り合う数の比が無限大の極限でφと一致する。
φは、正５角形の頂点を結ぶ線どおしが分割する比であり、歴史的建造物（ピラミッド、パルテノン神殿、五稜郭なども）に見られ、また自然界には、準結晶（アモルファスと結晶の中間）、植物の葉の出方、巻貝の成長過程の履歴などに見られる。
もし黄金比にミステリアスなものを感じるならば、なおのこと ｅ、π、ｉ がどんなに不思議な数であるかを感じ取ってほしいと思う。
（２） 複素数の拡張の可能性が無いこと：
複素数をさらに拡張して、新しい数の体系を作れるか？を検討する。
四則演算が自由にできる数の体系で、”ｎ 次元の数”が もしあれば、
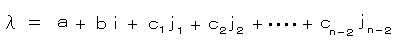
ただし、 ａ、ｂ、ｃｉ は実数、 ｉ は虚数単位、 ｊｉ は”新しい数”の単位
で一意的に表されるはずである。
この式の λ の ｎ 乗をつくり、
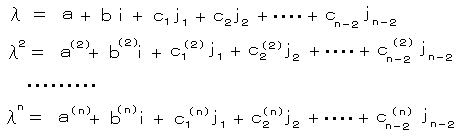
ｉ 、ｊｋ を消去して λ についての式にまとめると、
（ａｉ 実数） １）となり、 λ は実係数の方程式の解となる。
係数を複素数に拡張し、１）の方程式を満たすから ｋ＜＝ｎ
２）そこで複素数αを、
３）を満たすようにとる。
因数分解の公式
ｍ＝１、・・・、ｋを用いて、２）から ｚ＝αとおいた３）を引いて、λ について整理すると、（ここで乗法の可換性を用いている）
ここで γ はαを含む式で、複素数。αｋは０でないので、
ゆえに、
したがって、”ｎ次の数”ではないかと期待されていた λ は実は、複素数にすぎない事になる。
ⅰ） 四元数：
四則演算のうち、乗法の可換則が成り立たない条件で、四元数（ハミルトンの四元数）
、 （ａ、ｂ、ｃ、ｄ 実数） を定義することができる。単位 ｉ 、ｊ、ｋ の乗法について次の規則をおく。
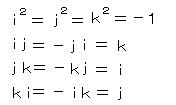
λ に対して
とおくとノルムは
となる。λ が０でないとき、１/λ は存在して、
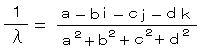
したがって、四元数の中で（非可換であるが）除法ができる。
除法ができ、かつ実数をスカラーのように乗ずることができる数の体系（実数体上の多元体）は、実数、複素数、四元数のみである。
四元数の積 (a0,a1,a2,a3)(b0,b1,b2,b3) = (a0b0-a1b1-a2b2-a3b3, a0b1+a1b0+a2b3-a3b2, a0b2+a2b0+a3b1-a1b3, a0b3+a3b0+a1b2-a2b1)
ｃｆ． 複素数の積 (a0,a1)(b0,b1) = (a0b0-a1b1,a0b1+a1b0)
ⅱ） 八元数：
八元数では交換法則も結合法則も成り立たない。
八元数の積 (a0,a1,a2,a3,a4,a5,a6,a7)(b0,b1,b2,b3,b4,b5,b6,b7)
= (a0b0-a1b1-a2b2-a3b3-a4b4-a5b5-a6b6-a7b7, a0b1+a1b0+a2b3-a3b2+a4b5-a5b4+a7b6-a6b7,
a0b2+a2b0+a3b1-a1b3+a4b6-a6b4+a5b7-a7b5, a0b3+a3b0+a1b2-a2b1+a4b7-a7b4+a6b5-a5b6,
a0b4+a4b0+a5b1-a1b5+a6b2-a2b6+a7b3-a3b7, a0b5+a5b0+a1b4-a4b1+a7b2-a2b7+a3b6-a6b3,
a0b6+a6b0+a2b4-a4b2+a5b3-a3b5+a1b7-a7b1, a0b7+a7b0+a3b4-a4b3+a6b1-a1b6+a2b5-a5b2)