(1) 統計作用素の基本的な性質
① 定義;
混合状態 ・・・ 干渉し合わない部分を含むいくつかの部分系の集合。
純粋状態 ・・・ 完全に干渉している状態で、状態ベクトルで表現できる。
* 統計作用素(密度行列)

これは、状態のあらゆる可能性を含ませた形式で、純粋・混合の両方を記述できる。
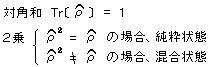
これは、純粋か混合かの評価方法になる。
統計作用素を用いた運動方程式は、
② 統計作用素のユニタリ変換;
時刻 t より未来 t' ( > t )において、
とすると、
ゆえに、閉じた系が、純粋状態ならばいつまでも純粋状態、混合状態ならばいつまでも混合状態
③ 全系と部分系の違い;
1) スピン1/2 の2つの粒子(2つの部分系)の場合、全系の任意の状態ベクトルは、
の、一次結合で表される。(重ね合わせの原理の一例)
ただし、α、βは粒子のスピンの状態(スピンの向き、上、下)、1、2は粒子1、2
統計作用素は、

2) 1)の設定で、全系のスピンが相殺して0である場合、スピンに関する状態ベクトルは、
この部分系1(粒子1)の状態を表わす統計作用素は、
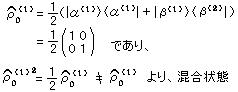
∴ 全系が一つの純粋状態であっても、一般に、その部分系は混合状態である。