　　　　　　　　２．　物質波と指数関数

　　物質は粒子であると同時に、波動でもある。これは最も認識しにくい事柄であるが、２０世紀初頭になされた電子線の干渉実験で発見され、その後も物性の実験やあらゆる素粒子における実験で確認され続けている。素粒子の波動は、実際は ”波束”という形をとっている。粒子性は、測定時波束が収縮して１つの量子的特性（質量、電荷、スピンなど）を持つ素粒子として振舞うことによって見られる。

　　波動関数が複素数であることは、量子力学の中心的な特徴である。
　　力学振動ではエネルギーが運動エネルギーと位置エネルギーの間を往復し、電気振動では電場のエネルギーと磁場のエネルギーの間を往復する。量子力学の波動関数の振動は、実数部と虚数部との間の往復となり、このような振動は古典物理学には存在しない。たとえば、
　　　　　　　
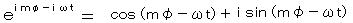
　　　　　　　　　　　　　　　　　　　　　　ただし、φ：水素原子のｚ軸上の回転角、時間因子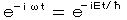

　　この複素数の波としての性質から、自然な形で、物質の空間的存在の”不連続性”（量子性）、また物理量の観測時の”不確定性” が導かれる。物質の背後にある複素数の波動関数を扱うので、数学上の３定数（神の３定数：ｅ、π、ｉ ）が常に基本的に存在する。

　　（波束、不確定性関係　→　（参考）３．（２）不確定性原理）

　　　（１）　物質波：

　　座標ｑにおける粒子の運動量ｐ（運動エネルギーＥ＝ｐ2/（２ｍ））というベクトルを考えると、それと同じものを表わす波としての性質をもつベクトルｋ（波数ベクトル）を、
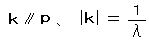　　　　　　　（λ：波長）　とおくと、

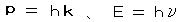　　　　　　　　　　　　　　　　　　（ν：振動数）

　　のように定義し、運動量（ｐ）と運動エネルギー（Ｅ）が波によって表現できる。ここで、ｈは プランク定数（6．547×10 ‐27ｅｒｇ・ｓ）であり、波と粒子を結びつける基本的な物理定数である。

　　波動を表わすならば、数学からそのまま神の３定数 π、ｅ、ｉによる指数関数の形になる。
　　波数ベクトルｋと振動数 ν をもつ平面波は、　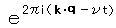　　で表わされるから、物質波の波動関数は
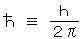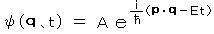　　　　　　　とおいて　　　　　　　　（波動関数の式）

　　この状態における粒子の存在確率は、　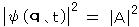　　　（＝定数）　　より、

　　この式は空間座標にも時刻にもよらない 無限に一様に広がっている平面波を表わしている。

　　（干渉を起こすための条件として、格子間隔が波長程度である必要があるので、通常、電子は粒子と考える。10000Ｖで加速した電子の波長は３×１０-10ｃｍ、振動数は３×１０18ｓ-1 。結晶の格子間隔は１０-8ｃｍ程度。この程度の速度ならば相対論的効果は考えなくて良い。）

　　また、ある時刻における粒子の存在範囲が重要な場合は、ｐを連続的に変えたものを重ね合わせて ”波束”を作る事ができる。粒子の存在形態のほとんどはこの波束である。

　　　（２）　シュレディンガー方程式：

　　外部からのポテンシャルＶ（ｑ）＝ 0 であるとき、粒子は自由粒子になり、その波動関数は（１）の波動の式あるいはそれを重ね合わせたものになる。これを座標ｑの成分および時間ｔで偏微分して整理すると、

　　　　　　　　　　　　　　　　　　

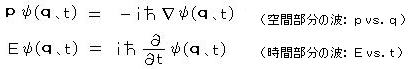
　　ポテンシャル Ｖ（ｑ） を含む場合は（座標のみにより時間によらないものとする）、エネルギーの次元をもちポテンシャルを含む場合もエネルギーにおき換えられるものとして、ハミルトニアン（エネルギー関数）Ｈを用いて運動エネルギーと位置エネルギーとの和の形で表わすと、
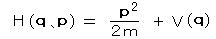　　　　　　となるから、　ＥをＨに、ｐを上式ｐψ（ｑ、ｔ）におきかえると、

　　　　　　　　　　　　　　　　　　　　
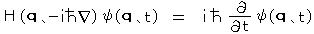
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（シュレディンガー方程式（1926））

　　１）　全体のエネルギーが一定の場合、ハミルトニアンは一定のエネルギーＥでおき換えることができるから、
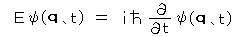　　　　　　　　　　　　　　　　　　　　　　　　　（上式と同じ形）

　　２）　時刻ｔは座標ｑによらず独立しているので、
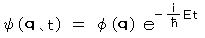　　　　　　　　（＊）　のように時刻ｔによらない関数 φ（ｑ）が分離され、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　
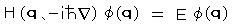
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（時刻を含まないシュレディンガー方程式）
　　特に、この式は　Ｈ（ｑ、ｐ）の式を用いて、

　　　　　　　　　　　　　　　　　　　　
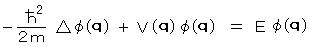
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ただし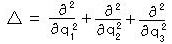　
　　の形に書くことができる。
　　（式の形は数学的にはポアソン方程式　　△φ（ｘ、ｙ、ｚ）＝ｆ（ｘ、ｙ、ｚ）　（ｆは既知の関数）である。）

　　たとえば、水素原子の場合、陽子によるクーロン引力のポテンシャルは　Ｖ（ｑ）＝－ｅ2/ｑ　（ｑ＝ｌｑｌ）で与えられる。（陽子は電子の1836倍の質量を持ち静止しているとして近似できる）

　　　（３）　指数関数の表れ：

　　物質の背後にある存在が”波”であるならば、当然、すべての性質に、数学上の３定数（神の３定数 ・・・ ｅ、 π、ｉ ）が現れる。

　　１）　　波動関数の 時間項は、初めに変数分離され全く独立に解かれる。

　　したがって、時間変数は何物にも支配されず、２重構造のどちらをも貫いて、あらゆるパラメーターの中で唯一１方向的に流れている。（相対論による時間の伸縮はあるが決して逆転することはなく同じ方向の流れである。
　　また、意識も霊の世界をも同時に貫いて支配している。（黙１２：１２））
　　ただし、不確定原理により、時間についても一般に実現確率の広がりをもって観測される。
　　波動関数の時間部分のｈを本来の形に、素直に書くと、　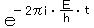　であり、（１）の平面波の式で振動数 ν ＝Ｅ/ｈとおいたものになる。
　　このように、自然は、すべての粒子が時の流れに従って、指数関数にある神の３定数 π、ｅ、ｉによって常に躍動的に実数と虚数との間を振動していることを示している。

　　２）　　次に、量子論特有の 空間的な不連続性も座標と波数ベクトルの内積を指数とする 指数関数の持つ多価性から自動的に導かれる。極座標表示の伏角 φ が変数分離され、その解、
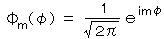　　　　　より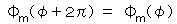　　　　
　　　　すなわち、　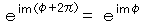　　　　　　　　∴　　　磁気量子数　　ｍ＝ 0、±1、±2、・・・　　
　　これから方位量子数ｌ、主量子数ｎによる不連続性が導かれる。逆に、ｎを指定すると、ｌ、ｍは自動的に導かれ、その上限、下限が決まる。（　→　水素原子　）

　　さらに、角運動量の行列表現によると、φ を２π だけ回転したときに要求されるのは行列要素の不変性のみなので、　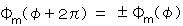　であればよく、　　ｍ＝ ±１/２、３/２、・・・も許され、この半整数はスピン量子数ｓを表わす。（スピンはディラック方程式（相対論的量子力学）から導かれるだけではない。）

　　３）　　さらに、空間的に不連続ではあるが、それらが指数関数を含む広がりをもって分布している。たとえば水素原子の解で、基底状態 ψｎｌｍ＝ ψ100 では、
　　　　　　　
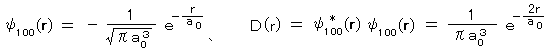
　　どんなに離れていてもわずかな確率で物質が存在しうる。（存在確率は 0 にはならない。薄膜（ポテンシャルの壁）も通り抜ける。）