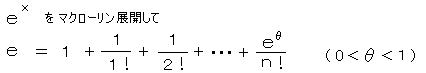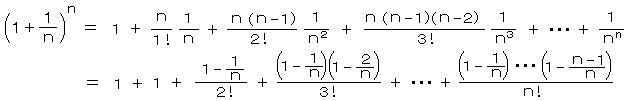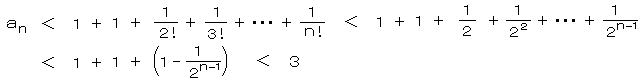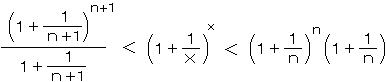２． 自然対数の底 ｅ の定義
π も ｉ も使わないで、純粋に解析的な方法（微分）から定義される、”自然対数の底（てい）” ｅ は最も神秘的な数である。なぜなら、何の変哲も無い数直線上の 約２．７ あたりに忽然と現れ、（０や∞のように明らかな特徴を持つわけではなく、） それが数学という”思索”の上で中心的な不動の役割を担っているからである。
確かに ｅ は、一つの 無理数（＊）であるのみならず、超越数（＊＊）である。しかし、このことだけで、ｅ は単独ではほとんど意味を持たない。ところが、 ｅ が複素数の”指数関数”として用いられると、残りの数学定数の π や ｉ に関わって 爆発的な発展性を 思索や物理の全体にもたらすのである！。
指数関数は、複素数という完結した数の体系（→ ６．）において、”正則性”という厳しい制約の元で自由に振る舞うことのできる、唯一の超越関数である。（→ ３．） また、自然界にはこの 指数関数 がいつも現れ、ほとんどすべての物理理論にあって（→ ３－2）、 ｅ は非常に堅い、不変の基盤を築いている。（たとえ宇宙が大爆発しても、死の ｅ として永遠に残るほど。最もしぶといのが、この ｅ である。）
ところがこの数には、歴史的経緯からか、直接的な名前が付けられていない。あまりにも”聖なる名前”なので、数学者であり神学学士でもある敬虔なオイラーやその他の数学者たちも遠慮してこうなったに違いないと思われる。オイラーの定数 γ （→ ４．）とは別物。（円周率、虚数単位、に対して、”自然対数”の”底”。バカボンのパパみたいな名前。これで ｅ のだ。）
・・・ 人として来られた大工の子 イエス様は、実は神のひとり子だった。 しかし イエス様は （ご自身の権威を行使せず、模範を示すために） 聖霊様に頼って 父なる神を解き明かし、主の栄光を世にあらわした。 そして、この世が終わって次の世がくると、イエス様は新しい名前を名乗られる（黙３：１２、黙２：１７）。
まず、純粋に ”極限の思索”（解析的思索）から導かれる ｅ 単独の素性について考える。
（ ｅ ＝ ２．７１８２８１８２８４５９０４５２３５３６０２８７４ ・・・・ ）
（１） ｅ の定義４つ：
１）～４）のいずれを用いても ｅ を定義することができる。
１）
・・・・ 通常の定義２） 無限級数の和
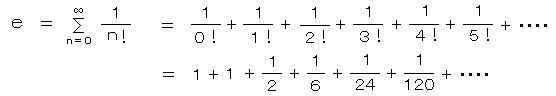
３） 指数関数の微分
を満たす ｅ４）
１/ｘの積分
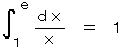となる数 ｅ（２） 通常の定義式（（１）の１））の導き方：
一般の指数関数
の逆関数は、対数関数と呼ばれ、 
で表される対数関数の導関数を考えると、微分の式
に代入して、
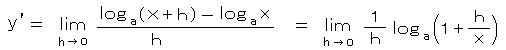
ここで、 ｈ/ｘ＝ｕ と置くと、
対数の中の項は、ｕ→０ の極限で ある実数値に収束することが証明されている（＊＊＊）。これを ｅ と置くと、
ここで、ｕ ＝ １/ｎ と書きかえると、ｅ の定義式になる。すなわち、 ・・・ ｅ の定義式ｅ を底とする対数関数は ｌｎ で表され、自然対数と呼ばれる。（あるいは数学では ｅ を省略して、ｌｏｇ ｘ で表すことも多い）
で表すと、上記 ｙ’は、
底 ａ ＝ ｅ の時、
（３） 指数関数の微分
の証明（（１）の３））同様に、微分の定義式より、
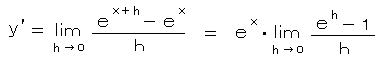
ここで、上記の ｅ に収束する式
を用いて、両辺の対数をとれば、
とおくと、
したがって、
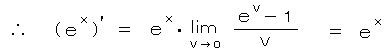
（４） 無限級数の和の証明（（１）の２）） （・・・ テーラー展開の式を使わないで）
指数関数の、微分しても変わらない性質
および、ｎ乗の微分
の２つより、
を証明する。
と置けるとする。これに 逐次微分
を行い、ｘ ＝ ０ を代入すると、右辺はすべて１になるので、次のようにそれぞれの係数が導かれる。
であると仮定すると、 ｎ － １ ＝ ｐ （ｎ 自然数）ととり、両辺に （ｎ － １）！ をかけると、 仮定より 左辺は 自然数である。
∴ ｐ ＝ １
（ｎ 自然数） なる極限値が存在することの証明：
・・・・・・ ①
とおくと、
とおけば、 
より、 不等式の両側に挟まれた形で ｅ に近づく。