5-2 複素積分の実例:
複素平面上における積分路積分を考えるとき、コーシーの積分定理が用いられる。このとき、正則な関数は 第1定理により項が消去され、特異点を含むものは第2定理の式が適用され、結局、虚数項が皆消えてしまう!。
聖霊様が働かれて、”実”が残る!。
(複素積分の理論については、5-3 ”コーシーの積分定理”参照)
(1)
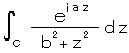 について、 右図のような積分路 C をとる。
について、 右図のような積分路 C をとる。
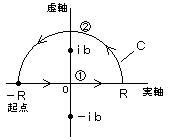
① C
の実軸部に沿って、 z = x
② 半円周の弧に沿って 、 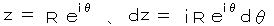
x = R のとき、 θ = 0 、 x =
-R のとき、 θ = π
これは、 R → ∞ の極限の場合に対し、a と b
(正の定数)をもつ。
①と②の積分路の積分に分けると、
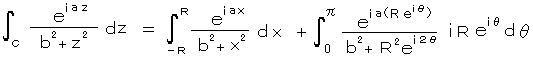
・ 左辺は、
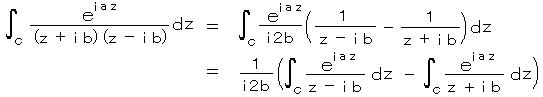
この第2項は、 z = -i b の特異点は 図より C の外側にあるから、この領域で関数は正則なので、コーシーの第1定理より、=
0 となる。
第1項は、 z = i b の特異点は、 b < R → ∞ で 常に C
の内側にあるようになるので、コーシーの第2定理
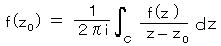 で
で 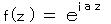 、 z0 = i b とおいた場合だから、
、 z0 = i b とおいた場合だから、
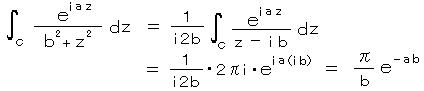
・ 右辺は、第2項(θ
の積分の項)
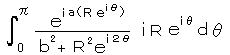 は、 R → ∞ で 0 に収束する。(*)
は、 R → ∞ で 0 に収束する。(*)
したがって、右辺の第1項だけが残り、さらにオイラーの関係式より、
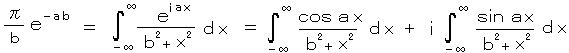
ここで 実・虚等値より、この第2項(sin
の項)は = 0 になる。
結局、最後まで残ったのは、両辺とも実部のみで、
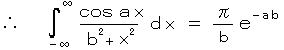 ・・・ (a 、b は正の実数)
・・・ (a 、b は正の実数)
特に、
a = 1、 b = 1 のとき、
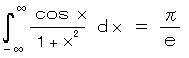
これは、重要な神のメッセージを含み、数学の基本定数 e 、π と ∞
を含む単純でエレガントな式である。
( → 7.)
*
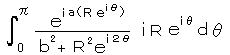 が R → ∞ で 0 に収束することの証明:
が R → ∞ で 0 に収束することの証明:
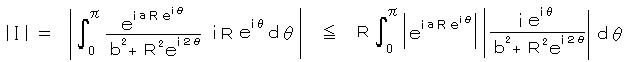
b2 を消して、
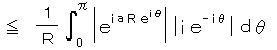
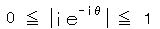 より、
より、
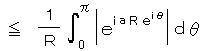 オイラーの関係式より、
オイラーの関係式より、
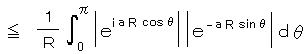
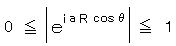 より、
より、
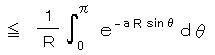
ここで θ が 0 から π で 常に 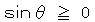 より、
より、
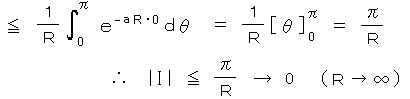
(2) コーシーの第1積分定理による フレネル積分の導出:
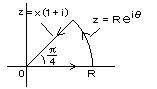
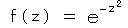 を図の楔形の積分路で解く。
を図の楔形の積分路で解く。
実軸正の方向に沿って z = x 、 dz = dx 、
1/4 円弧に沿って z = Rexp(iθ)、 dz = i
Rexp(iθ)dθ、
戻る直線に沿って z = (1+ i)x 、 dz = (1+
i)dx
f(z) は全複素平面で正則であるので、コーシーの第1定理より、
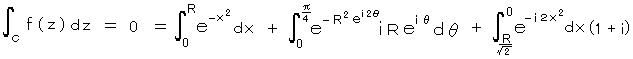
右辺の第1項は、
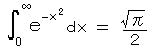 であることが知られている。(ガウス積分の半分、5.の(1)より)
であることが知られている。(ガウス積分の半分、5.の(1)より)
第2項は、R → ∞ で 0 になる。(**)
したがって、第3項については オイラーの関係式より、
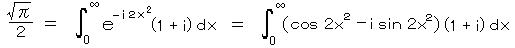
実虚等値すると、
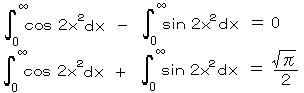 より、
より、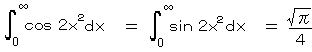
変数を θ2 = 2 x2 とおくと、
∴ 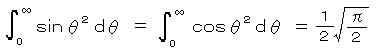 (フレネル積分)
(フレネル積分)
( ・・・・・ 5の(2)の結果と同じ)
** I = (右辺 第2項) とおくと、
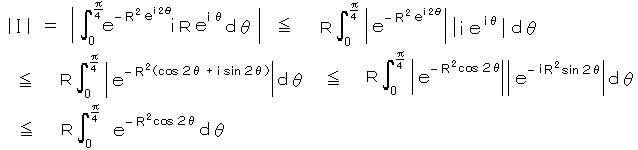
φ = 2θ におきかえると、 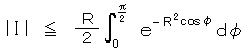
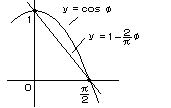
ここで 図より、 φ が 0 から π/2 の間で、直線 y = (2/π)(π/2-φ)
= 1 - (2/π)φ が y = cos φ よりも常に下にあるので、
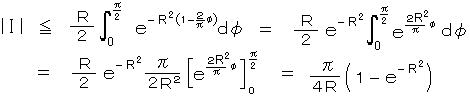
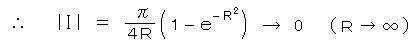
(3)
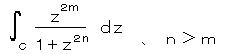 ただし n、m は非負の整数 について解く。
ただし n、m は非負の整数 について解く。
被積分関数の特異点は、 円分方程式 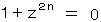 の解で、 ド・モアブルの定理より、
の解で、 ド・モアブルの定理より、
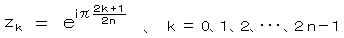 ・・・ 1)
・・・ 1)
の 2 n 個あって、複素平面の単位円周上を分割している。
(1)と同様に 半径 R、角度 0 から π の半円形の積分路をとると、
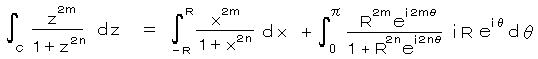
右辺第2項は n > m より、 R^2n は少なくとも R^(2m+1) よりも 1次多いので、 R → ∞ のとき 0 になる。したがって、
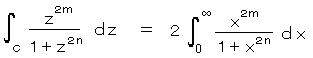 ・・・ 2)
・・・ 2)
ここで 左辺について、
被積分関数の部分分数展開として書くと、2 n 個の 特異点はすべて 1次であって、
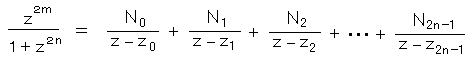 ・・・ 3)
・・・ 3)
とおける。 ここで、 Nj は定数とおく。
積分路は 上半分の半円なので、積分を 上半分と下半分にある特異点によって分けると、
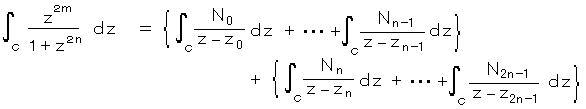
zn から z2n‐1 までの特異点は、積分路の外部にあるので、 コーシーの第1定理より すべて 0 になる。
また、 z0 から zn-1 までの特異点は、積分路の内部のあるので、
コーシーの第2定理の f(z) = 1 、 f(z0) = 1 とおいた場合で、
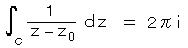 より、
より、 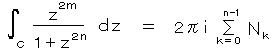 ・・・ 4)
・・・ 4)
N p 、 0 <= p <= n-1 とおく。 3) に (z - zp) をかけて、すなわち、
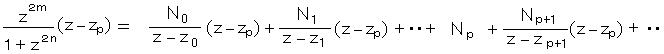
において、 z → zp とすると 右辺の Np 以外の項は すべて 0 になるから、
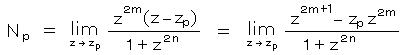
ここで、 ロピタルの規則 limx→x0 f(x)/g(x) = limx→x0 f’(x)/g’(x) より、分子、分母をそれぞれ微分した極限は、
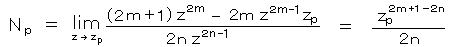
zp に 1) を代入して、
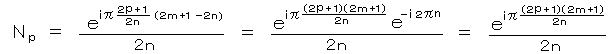
したがって、 2) 4) より、
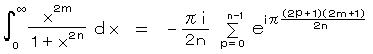
この総和は 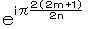 を 公比とする 幾何級数になっているから、オイラーの関係式を用いて整理し、
を 公比とする 幾何級数になっているから、オイラーの関係式を用いて整理し、
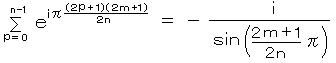 が導かれる。
が導かれる。
したがって、 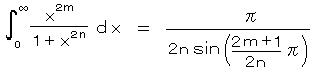 、 n > m ・・・ 5)
、 n > m ・・・ 5)
5)式で、 α = 2 m + 1、 β = 2 n とおけば、
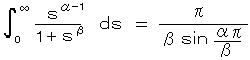 (一般的な形)
(一般的な形)
( ・・・・ オイラーの反射式を導くのに用いられた式(5-1(4)))となる。
5)式で、 m = 0、 n = 1 のとき、
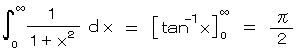 (よく知られた積分)
(よく知られた積分)
m = 0、 n = 2 のとき、
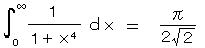 (5-3(4)の結果と同じ) などとなる。
(5-3(4)の結果と同じ) などとなる。
5.へ戻る 1.へ戻る
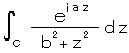 について、 右図のような積分路 C をとる。
について、 右図のような積分路 C をとる。
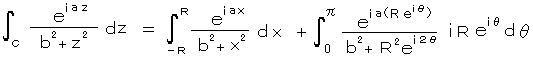
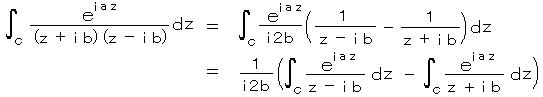
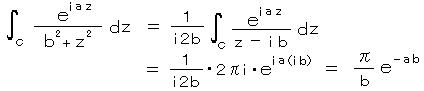
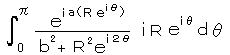 は、 R → ∞ で 0 に収束する。(*)
は、 R → ∞ で 0 に収束する。(*)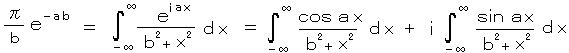
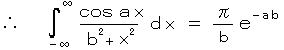 ・・・ (a 、b は正の実数)
・・・ (a 、b は正の実数)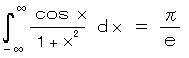
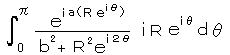 が R → ∞ で 0 に収束することの証明:
が R → ∞ で 0 に収束することの証明: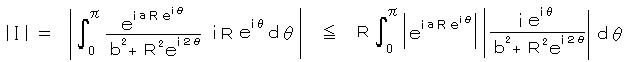
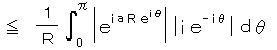
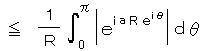 オイラーの関係式より、
オイラーの関係式より、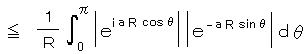
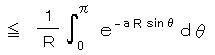
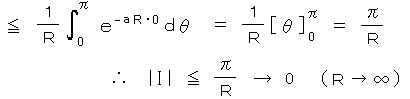

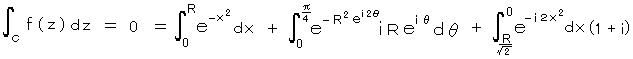
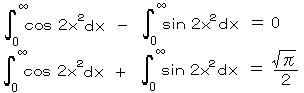 より、
より、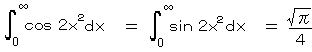
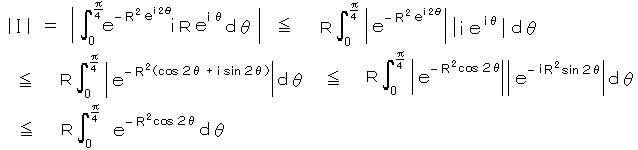
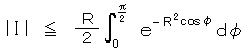

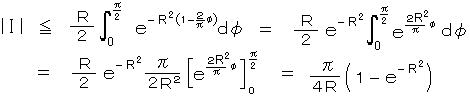
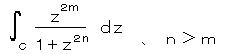 ただし n、m は非負の整数 について解く。
ただし n、m は非負の整数 について解く。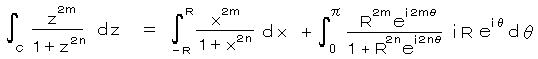
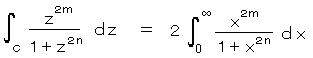 ・・・ 2)
・・・ 2)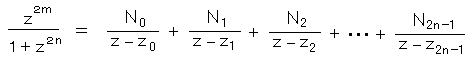 ・・・ 3)
・・・ 3)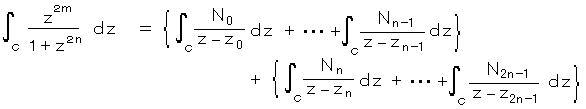
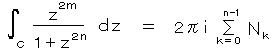 ・・・ 4)
・・・ 4)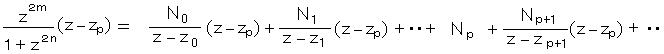
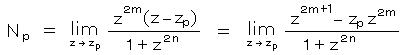
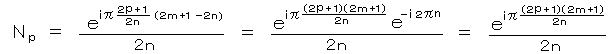
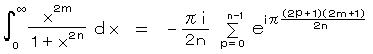
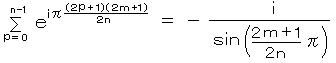 が導かれる。
が導かれる。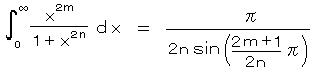 、 n > m ・・・ 5)
、 n > m ・・・ 5)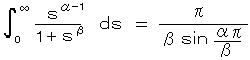 (一般的な形)
(一般的な形)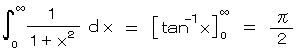 (よく知られた積分)
(よく知られた積分)