場の量子論の概略(1)
位置 q と運動量 p の不確定性関係は、それらの演算子の正準交換関係
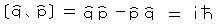
から導かれる。この正準交換関係が不確定性関係の最も基礎的な表現であり、自然(の水面下)の状態はプランク定数 h を介して複素数で記述される。驚くべきことに、自然の本質は複素数である。( → 自然の2重構造(確率性)、不確定性原理 )
この不確定性原理から、自然の4つの基本的な力が働くメカニズムが説明され、力を媒介する”新たな粒子”が常に瞬間的に生成消滅しているためであることが導かれる。
そして、自然のもう一つの性質、光速 c =一定、からスタートした相対論を導入した結果、反粒子やスピンといった素粒子の基本的な構造が自然に導かれるのである。
また、電磁場の根源的な場であるベクトル・ポテンシャルの発見に伴い、ゲージ理論が構築され、自然の対称性が明らかにされ、自然にある4つの基本的な力が統一されるべきものとして理解されるようになった。(重力の統一は未だ成功していない)
場の量子論による予測と高エネルギー加速器による実験から、現在、(それぞれの反粒子を除いて)17種類の基本粒子(* 場の量子論の概略(2)の下参照)が知られている。
ただし、場の量子論は、あくまでもすでに在る物質の”変換”を議論するものであって、無から有が生じることを言っているのではない。
1. 4つの基本的な力:
π 中間子の核力の到達距離は、不確定性原理から推定できる。運動量と位置の測定精度の不確定性関係 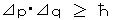 を変形すると、エネルギーと時間の測定精度の不確定性関係
を変形すると、エネルギーと時間の測定精度の不確定性関係 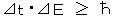 となり、短い時間 ⊿t の間にはエネルギーを正確に決めることができず、エネルギー保存則も
⊿E 程度は破れていてもよいことになる。すなわち、(ガンマ線顕微鏡の思考実験のように)当初は、不確定性原理が適用されるのは我々が知る観測上の情報についてだけと考えられたが、実際それがエネルギーや粒子の生成・消滅として、水面下の最も基本的な所に働いているのである。
となり、短い時間 ⊿t の間にはエネルギーを正確に決めることができず、エネルギー保存則も
⊿E 程度は破れていてもよいことになる。すなわち、(ガンマ線顕微鏡の思考実験のように)当初は、不確定性原理が適用されるのは我々が知る観測上の情報についてだけと考えられたが、実際それがエネルギーや粒子の生成・消滅として、水面下の最も基本的な所に働いているのである。
エネルギー保存則の破れ ⊿E は、 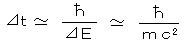 程度の短時間であれば許され(m は π 中間子の質量)、このようにして生成される平均寿命が短い粒子は”仮想的粒子”とよばれる。
程度の短時間であれば許され(m は π 中間子の質量)、このようにして生成される平均寿命が短い粒子は”仮想的粒子”とよばれる。
この π 中間子が光速(相対論で許される最高速度)で到達できる距離 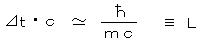 (L: コンプトン波長)が、π 中間子の交換によって生じる核力の効果が及ぶ範囲である。
(L: コンプトン波長)が、π 中間子の交換によって生じる核力の効果が及ぶ範囲である。
また、陽子と陽子の散乱断面積の測定値から、陽子の半径が R ~ 1×10-15(m) であり、核子の半径の2倍程度まで核力が及ぶ(L=2R)とすると、
π 中間子のもつエネルギーは、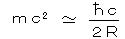 ~ 2×10-7(eV・m)/2×10-15 = 100MeV となる。(湯川の予言) 1947年に測定された値は140MeVであり、ほぼ的中した。
~ 2×10-7(eV・m)/2×10-15 = 100MeV となる。(湯川の予言) 1947年に測定された値は140MeVであり、ほぼ的中した。
π 中間子の交換による核力ポテンシャルは、場の理論によって導かれ、
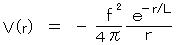
となり、 r が L の数倍以上では指数関数 exp(-r/L)によって急速に減少する。(湯川ポテンシャル) f は、π 中間子と核子との結合の強さを表す定数(強い相互作用の結合定数)であり、核力のポテンシャルの強さは f2 で決まる。
一方、2つの単位電荷 e の間に働く クーロン・ポテンシャルは、
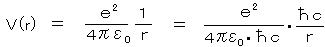
より、1/r で減少しながら r = ∞ まで達する。これは、荷電粒子の間に交換される光子の質量が0であり、プランク定数 h によらないことに起因する。電荷 e は、光子と荷電粒子との結合の強さを表す定数という解釈ができ、電磁相互作用の結合定数と呼ばれる。
核力と電磁力のそれぞれの結合定数を比較すると、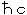 ~2×10-7(eV・m)より、
~2×10-7(eV・m)より、
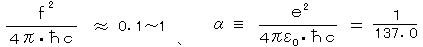 (MeV) (α: 微細構造定数)
(MeV) (α: 微細構造定数)
となって、f2 は e2 の10~100倍大きいことがわかる。
(* 強い相互作用は、さらに基本的には、グルオンとクォークとの相互作用の結合定数による(→ 下図))
重力ポテンシャルは、 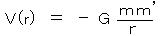 であり、 G = 6.673×10-11(m3・kg-1・s-2) = 6.707×10-39・
であり、 G = 6.673×10-11(m3・kg-1・s-2) = 6.707×10-39・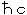 (GeV/c2)-2、陽子の静止エネルギー Ep = 940MeV、R = 10-15mとして、核内レベルの陽子と陽子の間の重力ポテンシャルの大きさで比較すると、
(GeV/c2)-2、陽子の静止エネルギー Ep = 940MeV、R = 10-15mとして、核内レベルの陽子と陽子の間の重力ポテンシャルの大きさで比較すると、
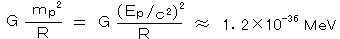 であり、核力、電磁力に比べ非常に小さい。
であり、核力、電磁力に比べ非常に小さい。
2. 相対論の導入(場の方程式):
非相対論のシュレディンガー方程式は、自由粒子の場合、
運動エネルギーの式 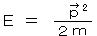 に、
に、 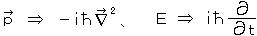 の演算子への置き換えをして、
の演算子への置き換えをして、
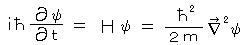 が得られた。
が得られた。
相対論の場合、このエネルギー E と、運動量 p の間に、アインシュタインの関係 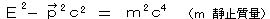 があるので、この式に同様に演算子の置き換えを行なって、
があるので、この式に同様に演算子の置き換えを行なって、
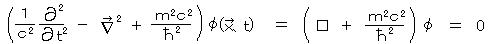 (クライン-ゴルドン方程式)
(クライン-ゴルドン方程式)
が得られる。(□はダランベルシャン)
この波動 φ を”場”と見ることができ、φ が複素数をとるとき”複素場”といい、この見方では”場の方程式”ということができる。
クライン-ゴルドン方程式の一般解は、無限に一様に広がる平面波(複素場)の重ね合わせ、
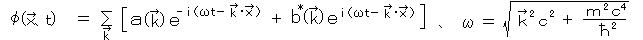 となる。(φ の複素共役は φ*)
となる。(φ の複素共役は φ*)
相対論の効果は、時間の係数 ω の中に エネルギーとして k→(運動) と m(静止) が含まれていることである。
cf. 非相対論: 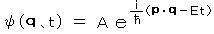
係数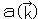 、
、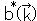 は複素数であり、演算子となる。
は複素数であり、演算子となる。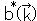 は、
は、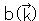 のエルミート共役
のエルミート共役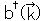 である。
である。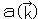 は、運動量
は、運動量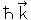 とエネルギー
とエネルギー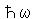 をもつ粒子を消滅させる演算子であり、
をもつ粒子を消滅させる演算子であり、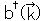 は、その反粒子を生成する演算子である。
は、その反粒子を生成する演算子である。
ただし、この方程式は、負のエネルギー解と負の確率密度が現れ、また、スピンが出てこない問題点があった。
* 自然単位系:
素粒子が関わる現象では粒子の速度は光速 c に近い場合が多く、相対性理論に基づいた記述が普通であり、同時に、いろいろな量を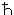 を基準として測る。そこで、 c =
を基準として測る。そこで、 c = 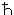 = 1 とする単位系(自然単位系)をとることにする。自然単位系では、たとえば、粒子の静止エネルギー m (←
mc2)、 スピン S=1/2 (←1/2
= 1 とする単位系(自然単位系)をとることにする。自然単位系では、たとえば、粒子の静止エネルギー m (←
mc2)、 スピン S=1/2 (←1/2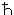 )、 微細構造定数 α=e2/(4πε0)、 コンプトン波長 1/m、 クライン-ゴルドン方程式
)、 微細構造定数 α=e2/(4πε0)、 コンプトン波長 1/m、 クライン-ゴルドン方程式 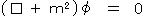 、などとなる。
、などとなる。
(* 神様の計量感覚は、我々の日常感覚(KMSA単位系でc :3.00E+8(m/s)、h : 6.63E-34(J・s))と比べ 42桁も違う!)
3. ディラック方程式とスピン:
Ag原子のビームが2つに分離するのは、最外殻の電子のスピンの状態が、 sz = ±1/2 の2種類あるためで、それぞれの波動関数を、 ψ1(x)χ↑、ψ2(x)χ↓ とあらわし、ψ は これらの重ね合わせで記述される。この波動関数を、パウリ・スピノルとよぶ。
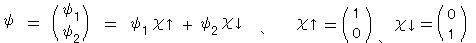
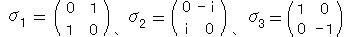 をパウリ行列とよび、スピン演算子は、
をパウリ行列とよび、スピン演算子は、 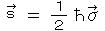 で表わされる。
で表わされる。
フェルミオンの粒子はすべて上記のシュレデディンガー方程式に従うが、t 微分の項は1次、∇の項は2次なので、ロレンツ変換に矛盾する。そこで、自由なスピン1/2の粒子の波動関数 ψ について、シュレディンガー方程式に代わるロレンツ不変な方程式を導く。
それは、1) ロレンツ不変性の要請から、t 微分の項、∇の項が、共に1次であり、 2) ψはクライン・ゴルドン方程式を満たす、という条件を満たす必要がある。
1)より、波動方程式は、α、β を適当にとって、
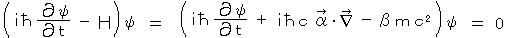 とおける。今、αi と β の間に、反交換関係
とおける。今、αi と β の間に、反交換関係
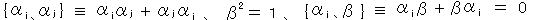 が成り立つとすると、クライン・ゴルドン方程式になって2)を満たす。そこで、この反交換関係を満たす
αi と β を求める。
が成り立つとすると、クライン・ゴルドン方程式になって2)を満たす。そこで、この反交換関係を満たす
αi と β を求める。
パウリ行列がこの関係式を、 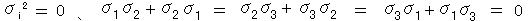 のように満たすので、
のように満たすので、
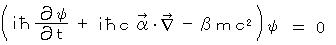
ただし、 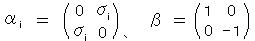 ・・・・ ディラック方程式(1928)
・・・・ ディラック方程式(1928)
が導かれる。
αi は 4×4行列、ψは ψ = (ψ1、ψ2、ψ3、ψ4) の縦ベクトル(ディラック場)である。非相対論では、電子の波動関数は2成分だったが、相対論では、電子の波動関数は4成分必要となることが分かった。
ディラック方程式に左から β/c をかけて、γ0 = β、γ→=βα→ とおくと γμ は、4×4のガンマ行列とよばれるものになり、ロレンツ不変であることが示される。
* 自然単位系(c=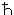 =1)におけるディラック方程式は、(すべて1次微分より、時間はμ0として縮約されて幾何学となり、)
=1)におけるディラック方程式は、(すべて1次微分より、時間はμ0として縮約されて幾何学となり、)
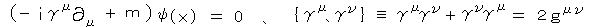 で表現される。
で表現される。
・・・ ψ は4成分スピノル、 γμ (μ=0、1、2、3)は4×4のディラック行列、 gμν はミンコフスキー空間の計量テンソル
自由なスピノル場の解を求める。自由なフェルミオンに対する ディラック方程式の平面波の解をつくるために、
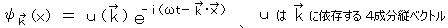 とおく。これをディラック方程式に代入すると、E =
とおく。これをディラック方程式に代入すると、E = 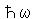 、p =
、p = 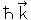 より、
より、 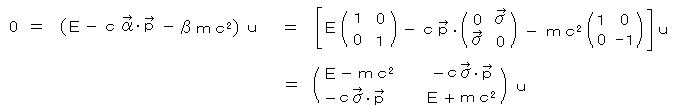
この式はハミルトニアンが4×4行列である固有値方程式 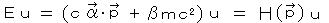 とみなすことができ、固有値 E は自由なフェルミオンのエネルギーを与える。 E を求めるために、H(p→)2 を計算する。
とみなすことができ、固有値 E は自由なフェルミオンのエネルギーを与える。 E を求めるために、H(p→)2 を計算する。
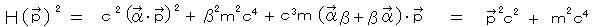
したがって、エネルギーの固有値は、 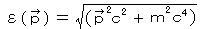 として、
として、 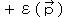 と
と 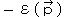 の2つある。
の2つある。
ここで、4成分スピノルを上成分、下成分に分けておく。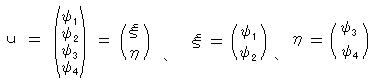
それぞれについて、固有値に対応する波動関数を求めると、
ⅰ) E = 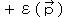 の場合:
の場合: 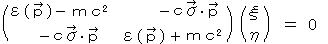
ここで、 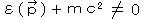 より、
より、 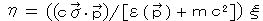 と求まり、
と求まり、
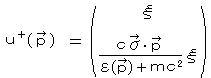 ・・・ 正エネルギー解
・・・ 正エネルギー解
ⅱ) E = 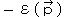 の場合: 同様に、
の場合: 同様に、
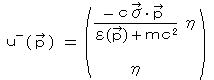 ・・・ 負エネルギー解
・・・ 負エネルギー解
したがって、4成分スピノルについては4つの独立した解があって、正・負という2つのエネルギー準位に対し、それぞれ上向きと下向きのスピンが2重に縮退している。
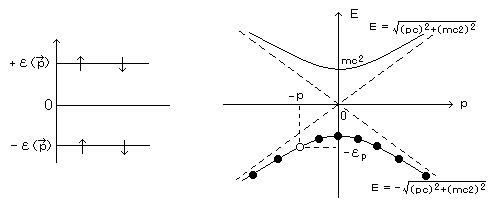
フェルミオンは、パウリの排他原理により、1つの状態には1つの粒子しか詰められない。ディラックは空孔理論を唱え、負エネルギー状態がすべて詰まっているエネルギーが最低の状態(”ディラックの海”)が真空を表わし、負エネルギー準位の空孔は、正エネルギーをもつ反粒子として観測されるとした。(図の○)
ディラック方程式の平面波の一般解は、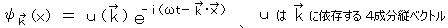 を重ね合わせて得られる。
を重ね合わせて得られる。
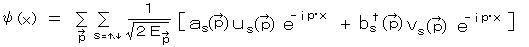
クライン・ゴルドン方程式と同様に、消滅演算子 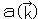 はあるエネルギー、運動量、スピンの向きをもつ粒子を消滅させ、生成演算子
はあるエネルギー、運動量、スピンの向きをもつ粒子を消滅させ、生成演算子 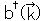 はそれと同じエネルギー、運動量、スピンの向きをもつ反粒子を生成すると解釈できる。ディラック粒子はフェルミ統計に従うので、生成・消滅演算子の間には反交換関係を仮定できる。すると、この反交換関係から
はそれと同じエネルギー、運動量、スピンの向きをもつ反粒子を生成すると解釈できる。ディラック粒子はフェルミ統計に従うので、生成・消滅演算子の間には反交換関係を仮定できる。すると、この反交換関係から  が導かれ、これは 2粒子が同一状態に存在できないことを意味し、すなわち、パウリの排他律を表わしている。
が導かれ、これは 2粒子が同一状態に存在できないことを意味し、すなわち、パウリの排他律を表わしている。
ディラック方程式は、負の確率密度は生じず、スピンの概念は自然に出てくるが、依然として負のエネルギー解の問題が残った。そこで、ディラックは”空孔理論”を考案し、この空孔による反粒子は後に陽電子(e+)であることが実験的に確認された。(1932・アンダーソン・陽電子を発見; ワイル、オッペンハイマー・反粒子が陽子ではなく陽電子であることを確認)
* 後のファインマン等による相対論的な場の量子論の発展によって、ディラックの海、空孔理論を考えなくても粒子・反粒子の問題が扱えるようになった。
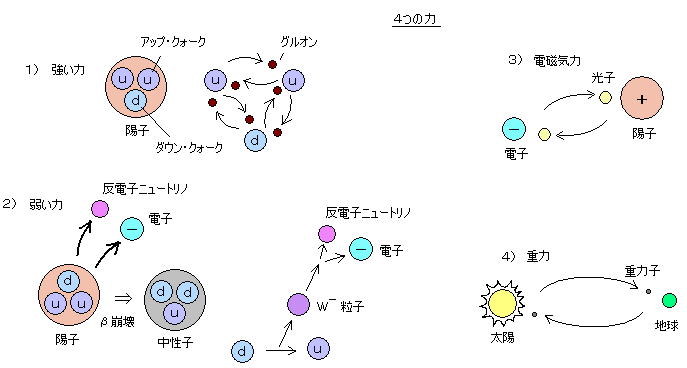
* 自然界に存在する4つの力:
力は場が伝え、その場は粒子でもある。マクロの自然界には、電磁気的な力と重力があるが、ミクロの世界でしか現れない”強い力”と”弱い力”が存在し、合計4つの基本的な力が知られている。場の量子論では、これらの4つの力はすべて粒子の交換によって働くと考えられている。
1) 強い力: 陽子や中性子の中で、クォークを結びつけている力で、原子核の中で陽子と中性子を結び付けている力はこの力がもとになっている。量子論では、グルオンという粒子を交換することによって働くとされる。
2) 弱い力: レプトンに関して働く力。ベータ崩壊のとき、W粒子を交換する弱い力が働くことにより、中性子が電子と反電子ニュートリノを放出して陽子に変わると考えられている。W粒子の存在は、加速器による実験で確かめられている。(**)
3) 電磁力: 光子を交換。
4) 重力: 重力子を交換するといわれているが、重力子(グラビトン)は特殊な粒子であり、ゲージ粒子ではない。
** W粒子:
通常は現れないが、高エネルギー加速器で加速された粒子を衝突させた場合に初めて現れてくる粒子がある。W粒子の質量は80GeVで、陽子の86倍もあり、不確定性原理から寿命は3×10-25s しかないが、加速した粒子同士をぶつけてW粒子のもつ静止質量エネルギー以上のエネルギーを発生させれば、一瞬姿をあらわしその存在を確認することができる。
次へ 1.へ戻る トップへ戻る
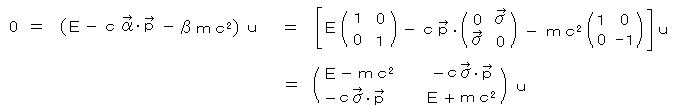
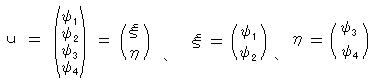
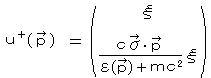 ・・・ 正エネルギー解
・・・ 正エネルギー解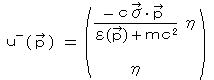 ・・・ 負エネルギー解
・・・ 負エネルギー解
