３． インフレーション理論の困難
（概要）
いわゆる”古いインフレーション理論”は、膨張宇宙論における地平線問題、平坦性問題を解決する目的で、アラン・グースによって提唱された。（1981） （彼の論文は、「地平問題および平坦性問題のありうる解決」） その問題解決のポイントは、プランク長程度の大きさから １０-35秒のごく短時間の内に急激に加速膨張するというものである。最初あまりにも極微なため、初期の粒子相互の因果律が保たれ、因果律の無くなる後の宇宙の背景放射の強さが同じとなる。また、膨張開始後１秒後の
Ω ＝ （宇宙の密度）/（臨界密度）は １±１０-15 の精度が要求されるが、インフレーションによる宇宙の直径の膨張率が少なくとも
１０30 オーダーで急激に膨張するため充分相殺され、後の宇宙は充分大きく広がったので我々が見える宇宙はごく一部のものとなって、ほとんど平坦になり、このようにして平坦性問題は解決したとする。
原初の火の玉宇宙の膨大なエネルギーの起源は、初めの”ニセの真空”とよばれる高次元・高エネルギーの真空が崩壊する時、インフラトンという仮想的な粒子がそのインフラトン場のポテンシャルの壁をトンネル効果によって通って現れ、極短時間の膨張途中で、対称性が破れ
重力を含む４つの力が分離し、３次元空間に膨大なエネルギーを供給する、というストーリーである。（→ ４つの力の統一理論） また、そのとき同時にできる重力場が負のエネルギーとなるため、エネルギー保存則が保たれているとする。
しかし、インフラトンという仮想的な粒子の正体については何も分かっていない。
ここで、観測の結果、背景放射には １０-5 程度の 方向によるゆらぎがあることが分かり、このインフラトンの零点振動によるゆらぎが、余りにも急激な膨張のためハッブル半径から一度出て、そのとき空間に凍りついたことが原因になっているとして理論展開がなされている。しかし、そのゆらぎの見積り値は余りにも大きすぎるので、観測値に合わせるために、”新しいインフレーション理論”として、インフラトン場のポテンシャルが極めて平坦であるものが提唱されている。これにはパラメーターを微調整する必要があるため、ビッグバン宇宙の平坦性問題（＝微調整問題）の代わりに
別の形での微調整問題の困難となっている。（→ 下の参考）
（１） 問題解決のポイント：
インフレーションの極短時間の急激な膨張は、後の宇宙の元素生成、宇宙背景放射、あるいは銀河生成などのシナリオとつじつまを合わせるためである。
プランク時間（１０-43秒）、プランク長（１０-33ｃｍ）（量子論によって、これ以上小さいものは想定できない時間と長さ）程度の急激な膨張を想定している。（ｃｆ． 原子の大きさ： １０-8ｃｍ、小さい原子核： １０-13ｃｍよりもはるかに小さい） インフレーション開始から １０－４３秒後、重力が他の力から分かれとき、時空という考え方が意味をもつようになった。さらに、１０-36秒後に強い力が、１０-10秒後に電磁気力と弱い力が分かれ、このようにして、４つの基本的な力が分かれた。この間に、１０-33ｃｍほどの大きさだった宇宙が、１０-3～１０4ｃｍほどに大きくなった。これは、直径でおよそ１０30倍以上の膨張である。
そこで、±１０-15 の範囲内という 膨張開始後１秒後の Ω ＝ （宇宙の密度）/（臨界密度） の誤差は、この急激な膨張に飲み込まれ、宇宙は我々が見ている宇宙よりもはるかに大きく成長した。そのため、ほとんど平坦に見える現在の我々が見ている宇宙が 宇宙全体のごく一部であることになり、ビッグバンの平坦性問題は解決される。
また、非常にたくさんあったモノポールも、宇宙が余りにも大きく広がったので極端に薄められ、現在、宇宙の地平線内（我々から観測できる範囲）に１個程度しか存在しなくなり、したがって観測にもかからない。
宇宙は初めはハッブル半径よりもはるかに小さかったので、インフレーション前に因果関係があったから、現在因果関係の無い領域にも同じ背景輻射の強度を持つとして、地平線問題も解決している。
（２） 新たな問題点：
インフレーションが起こっていたとすると、現在の宇宙の曲率はほとんど 0 でなければならない。ところが、観測結果では、現在の宇宙の密度は ダークマターを入れても 臨界密度の１０～２０％しかない。そこで、インフレーションと矛盾しないように、宇宙全体にかかる斥力としての重力をあらわす
宇宙定数 Λ （アインシュタインが彼の”定常宇宙論”を正当化するため一時導入し、後に撤回した）を導入するのであるが、この宇宙定数の実態については何も分かっていない。
膨大な宇宙全体のエネルギーを担う インフラトンの正体については、全く何も分かっていない。（もし、このエネルギーレベルの直接的な実験を行なうとすれば、銀河系ほどの大きさの加速器が必要になると考えられている。） ただ、インフラトンが量子力学に従う何らかの粒子であるとして、その挙動が推測されているに過ぎない。 間接的には、４つの力が分離した時の相転移に伴って発生したという、当時の重力波を観測することが最も有力視され、観測プロジェクトが進行中であるが、重力波はきわめて微弱なため未だ観測にかかっていない。
観測の結果、背景放射には １０-5 程度の 方向によるゆらぎがあることが分かっている。このゆらぎを理論で見積もると、観測値（１０-5）よりも大幅に大きくなる。そこで、”新しいインフレーション理論”としてインフラトン場のポテンシャルを極めて平坦にせざるを得なくなる。すると、パラメーターの微調整が必要となり、せっかく平坦性問題（＝ビッグバン理論の密度比の微調整問題）の困難が解決したのに、再び 微調整問題が提示されることになる。
主流でないその他のインフレーション理論（超弦理論、量子重力理論など）は、３次元よりももっと多くの次元空間（２６次元、１０次元）が存在し、そのうちの３次元部分だけがインフレーションしたとするが、現実とのリンクが未完成で、実証不可能の机上の空論に過ぎない状況である。
（参考） インフレーションの初期ゆらぎ と 微調整問題
現在観測されている １０-5 程度の方向による背景放射のゆらぎは、もともとインフラトン場の量子力学的不確定性に起源をもつと考えられている。
インフラトン場のゆらぎによって 物質化し始める時刻が場所ごとに異なるから、あるハッブル体積中における平均的な場の値 φ が、宇宙全体の平均から ⊿φ だけずれていたとすると、時間の発展のずれは、
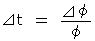
となる。 密度 ρ にもむらができ、 ρ ∝ ａ-3 （ａ： スケール因子） より、
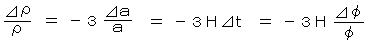
であり、 ⊿ρ/ρ ～ Ｈ⊿φ/φ のオーダーとなる。このように、インフラトン場のゆらぎにより、密度ゆらぎが与えられる。
ある振動子のモードについて、角振動数 ω、実空間のスケール １/ｋ とすると
ω ＝ ｃ ｋ であり、 ｒ ＝ ｍ-1/2ｃ-1｜φｋ｜ とおけば、
ラグランジアンは、
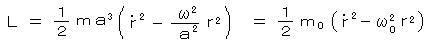
であり、全体のラグランジアンは、独立な１次元調和振動子の総和となる。
また、運動方程式は、
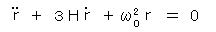
となる。これは、時間変化するバネ定数をもつ振動子が まさつを受けながら（まさつ係数 ３Ｈ）運動する系と等価である。
スケール ａ/ｋ が、ハッブル半径 ｃ/Ｈ（＝ 光速×時間 １/Ｈ）を超えているかどうかで場合分けし、
１） ａ/ｋ ＜＜ ｃ/Ｈ のとき： ハッブル半径内にある時は、まさつは重要でなく、周波数がゆっくり変化する、質量
ｍ0 、角振動数 ω０ の調和振動子となる。
この系を量子化した場合、基底状態の位置ゆらぎの期待値は、
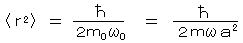（→ 零点振動）で与えられ、
フーリエモードの量子ゆらぎは、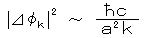 
となる。
２） ａ/ｋ ＞＞ ｃ/Ｈ のとき： ハッブル半径から出ると、まさつ項のみになり、運動は止まってしまう。すなわち、量子ゆらぎが一度ハッブル半径の外に出ると、このゆらぎの振幅は凍り付いてしまい、インフレーションが終わった時点 ａ ＝ ｃ ｋ/Ｈ の時、
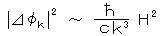というスペクトルのゆらぎが形成される。
ｋ3｜φｋ｜2/２π2 が実空間 １/ｋ における振幅であり、これはスケールによらず一定の振幅を持つ”スケール不変”のゆらぎとなる。したがって、密度のゆらぎは、
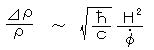
のオーダーとなる。
インフレーションが終了した後も、ハッブル半径を越えるゆらぎの振幅は変化しないため、再度 ハッブル半径に入ってきたゆらぎの振幅はほぼ一定になる。
しかし、この値が、観測されている １０-5 のゆらぎのオーダーのはずであるが、通常のインフレーションモデルの計算値はこれよりはるかに大きくなってしまう。
そこで、アラン・グース以降の「新しいインフレーション理論」では、インフラトンのポテンシャルが極めて平坦でなければならないが、パラメーターがかなりの微調整を要求される。すなわち、微調整問題（＝ ビッグバンの平坦性問題）が再び現れることになり、それを回避するために導入されたインフレーション理論はビッグバン理論と同じ困難に陥ることになる。
次へ １．へ戻る トップへ戻る