２． 数学の３定数（２）：
２） 代数学の ｉ ：
虚数単位 ｉ は、もともと代数方程式の根を求める際に、実数範囲では解がない場合にやむを得ず導入されたものであり、何か取って付けたような 全く直感することができない数である。ところが、不思議なことに、実数部とこの虚数部を足した”複素数”こそは、”四則演算”が自由にできる条件が 必要かつ十分となっている 数の体系（複素数体）である。もし、虚数単位のほかに新しい単位を追加するならば、四則演算の自由度を失ってしまう。（ → 四元数・八元数 ６．（２） ）
方程式の根（または、解）を求めるとは、その方程式を満たすような（無限の可能性のある変数の中からの）ある特定の数 ｘ を見出すことである。これは、帰納的な表現となっている。（さらに、微分方程式の場合は、無限の可能性のある関数の中からある特定の関数を見出す、になる。）
のようになる。一般に、有理数係数の方程式
（ａ1、ａ2、・・・、ａｎ は有理数）の解になる 複素数を代数的数という。・・・
などこれに対し、代数的数でない複素数を 超越数と呼ぶ。・・・ π 、 ｅ など。 また、代数的数の超越数乗は超越数。 ｅ の代数的数乗は超越数。 集合論によると、超越数のほうが代数的数よりも 数直線上に存在する密度がはるかに大きい。
・ 円積問題 ・・・ 半径1の円を同じ面積になるような正方形に作図する、という問題はギリシャ時代に提起され、直感的には解けそうであったが、ずっと後の時代に、 π が超越数であることが証明されてから、否定的に解決された。（ ｅ が超越数（ｴﾙﾐｰﾄ・1873）であることを用いて、π が超越数（ﾘﾝﾃﾞﾏﾝ・1882）であることが証明された。）
・ ド・モアブルの公式 ・・・ 複素数の平面表示（横軸に実数軸 ｘ 、縦軸に虚数軸 ｉ ｙ）をガウス平面と呼ぶ。
この 複素数の極座標表示を使って 単位円の ｎ 分割を考える。
・ 代数学の基本定理 ・・・ 任意の複素数係数の ｎ次の代数方程式
は、少なくとも１つの解を複素数の中に持つ。（ガウス・1799）
（（注） この ｆ（ｚ）＝０ が少なくとも１つの解を複素数の中に持つことが言えれば、剰余定理から自動的に、重解を含めて ｎ個の解を複素数の中に持つことが言える。）
複素数の範囲ですべての代数方程式を解くことができると同時に、複素数の拡張の可能性はこれ以上は無い、というのが、この定理の主張である。
四元数の乗法の可換性が否定されることによっても、複素数体 Ｚ は、私たちの通常の数学的感覚である”四則演算”に対し完結した体系である。（自然の構造についても、万物は本質的に複素数で構成されている。（量子力学））
虚数単位は、我々の直感では認識できない数であるが、このように、すべてを包括するもう一つの世界を明確に規定している。
３） 解析学の ｅ ：
さて、π、ｉ という準備ができた上で、”関数”を考える。自然対数の底（てい） ｅ が発見されたのは、π に比べかなり後の時代（１７世紀以降）であり、これは、歴史の途中から、明らかな形で ”御子イエス様”が現れたのと同じである。
１８〜１９世紀にかけては、物理学、天文学、化学などが著しく発展し、力学振動や電磁場、熱力学などの自然（＝被造物）を記述するのにふさわしい数学理論が求められていた。自然対数の底 ｅ は、その名の通り、あらゆる”自然”を記述するための基本となる定数である。
・ 導関数を次のように定義する。 ｘ を変数とする関数 ｙ ＝ ｆ （ｘ） の微分（＝導関数）は、
で与えられ、この ｘ における極限値は、その関数の”変化率”を表わす 新たな関数になる。解析学とは、微分や積分による関数の変化を扱う分野であり、微積分学や微分方程式論、複素関数論へと発展していった。 （微分・・・微かに分かる、積分・・・（ﾚ点を付けて）積ﾚ分、分かった積もり、と読む？）
ここで、微分しても全く同じ関数となる
となるような指数関数を考えると、この ｅ の値は、ある一定の無理数（２．７１８２８１８２８・・・）に定義される。（４つある定義の一つ → 自然対数の底の定義 （１） ） これを、自然対数の底と呼ぶ。この ｅ は、無理数であるのみならず、超越数でもある。・ 無限級数は、代数式（＝ 整式、代数方程式の左辺）を、無限次元まで拡張したものである。無限級数は、有限次元の整式が持っている性質をそのまま極限まで受け継ぐことができるが、収束することが条件である。
指数関数（自然対数の底 ｅ の指数関数を”指数関数”と言う）の場合、
のように展開される。（ｎ！： ｎ の階乗 ＝ １・２・３・・・・（ｎ−１）・ｎ ）
この 各 ｎ 次の項を何回微分しても、項の数は”無限”だから、順次 係数が打ち消し合って、結局、指数関数の形は全く変わらない。（積分についても積分定数を１ととって同様に変わらない）
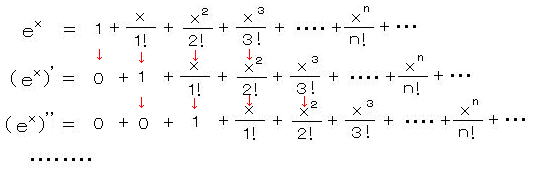
・ オイラーの関係式は、虚数冪の指数関数の展開式と 三角関数の展開式とを突き合わせて導かれる。この指数関数の冪に 純虚数 ｉ ｘ を代入すると、すべての奇数次の項が虚数になり、これを、偶数次と奇数次の項に分けると、それぞれ三角関数の展開式になる。
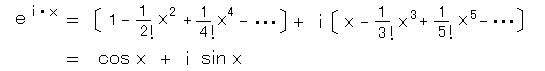
ｘ ＝ π のとき、あのエレガントな驚くべき関係式 ・・・ オイラーの恒等式が導かれる。
一般的に、指数関数の冪に複素数 ｚ を導入するには、無限級数展開をしてから、各項の ｘ の代わりに ｚ を代入して定義する。
これは 指数法則
が成り立ち、特に、実部と虚部で分けると、オイラーの公式となる。
・ ｅ の数値の計算は定義の通りである。
１）
２）
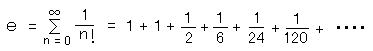
・ π の数値の計算は、オイラーの関係式を用いて行われる。（他にも方法があるが）
オイラーの関係式の ｘ に π/２ を代入して、
より、
メルカトルの式
を用いて、
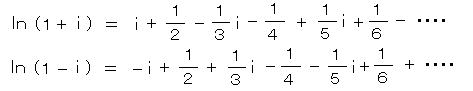
両式の各項どおしを引いて
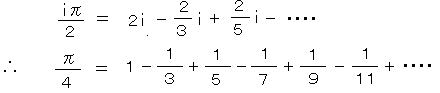（ｸﾞﾚｺﾞﾘｰ・1671）また、より収束の速い式も同様に導かれ、これは現在でも π の計算に用いられている。
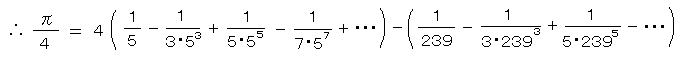
（ﾏｼﾝ・1706）
この式は、アルキメデス法よりもはるかに計算しやすい方法で、1949年に世界最初の電子計算機 ＥＮＩＡＣが πを２０００小数位以上計算した。（現在、π は約２０６０億桁、ｅ は約１３０億桁）
このように、ｅ 、ｉ が π の値を具体的に明らかにした！
・ また、ｅ が超越数であることを使って、π が超越数であることが証明された。（ﾘﾝﾃﾞﾏﾝ・1882）
「いまだかつて神を見た者はいない。父のふところにおられるひとり子の神（＝イエス様 ｅ ）が、神（＝御父 π ）を説き明かされたのである。」（ヨハ１：１８）